- (a)
- A single particle system has 3 non-degenerate energy levels 0,
0.02 and 0.05 eV. It is in thermal equilibrium with a heat reservoir at
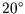 C. Calculate the partition function, the
probability that the particle is in each level and the average energy.
What is the average energy in the limit of very large temperatures
(
C. Calculate the partition function, the
probability that the particle is in each level and the average energy.
What is the average energy in the limit of very large temperatures
(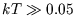 eV)?
eV)?
- (b)
- Now consider a similar system with the 0.02 eV level being two-fold degenerate and the 0.05 eV being three-fold degenerate, and repeat the question. Explain the differing values you get for the large-temperature limit of the energies.
In this question, we are just interested in the partition function as a
normalisation constant. For the high-temperature limit, ask yourself what
value the probabilities tend to as ![]() . See here.
. See here.
and the heat capacity by
Plot both these functions, find their low and high temperature limits, and explain your findings.
In this question, we use the partition function to caluculate other properties. The calculation is very like the two-state system, see here and, for details, here. Hazy on hyperbolic trig functions and their limits? See here
By considering entropy as a function of pressure and temperature, show that for any substance a change of entropy
where
Consider ![]() m
m![]() of mercury at 273K and atmospheric pressure
for which the heat capacity
of mercury at 273K and atmospheric pressure
for which the heat capacity
![]() JK
JK![]() and
and
![]() K
K![]() . You may assume to a good approximation
that
. You may assume to a good approximation
that
![]() and
and ![]() are independent of temperature and pressure and that
mercury is incompressible. The pressure on the mercury is now increased to
100atm. What is the change in temperature if the pressure change occurs
reversibly and adiabatically?
are independent of temperature and pressure and that
mercury is incompressible. The pressure on the mercury is now increased to
100atm. What is the change in temperature if the pressure change occurs
reversibly and adiabatically?
See here for a somewhat similar example of writing
![]() in terms of other variables, and also the question 8 on examples 2.
In the last part, the conditions are such that the entropy is constant,
in terms of other variables, and also the question 8 on examples 2.
In the last part, the conditions are such that the entropy is constant, ![]() , so we
have
, so we
have
![]() and hence
and hence
![]() .
(The question tells us we can treat
.
(The question tells us we can treat ![]() ,
, ![]() and
and
![]() constant.)
The temperature change is 0.26K.
constant.)
The temperature change is 0.26K.
See qu. 19 for the fundamental thermodynamic relation in this case.
We still have for the Helmholtz free energy ![]() , and the desired Maxwell
relation is derived from
, and the desired Maxwell
relation is derived from ![]() just as the one for
just as the one for
![]() is in a hydrostatic system. Part c) is similarto, but a bit more
involved thant, the example here. You will need to integrate
is in a hydrostatic system. Part c) is similarto, but a bit more
involved thant, the example here. You will need to integrate
![]() to get
to get ![]() , and then integrate
, and then integrate
![]() to get
the final result, which is
to get
the final result, which is
![]() .
.
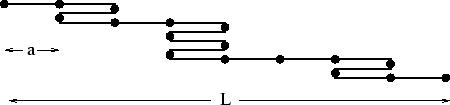
A simple model of a rubber band in one dimension is a chain of ![]() links each
of length
links each
of length ![]() . Each link may point to the left or to the right without any
difference in energy, as illustrated above. Hence if there are
. Each link may point to the left or to the right without any
difference in energy, as illustrated above. Hence if there are ![]() (
(![]() )
links to the right (left), we have
)
links to the right (left), we have
and the energy is independent of
Find an expression for the tension ![]() as a
function of the length of the band, and show that it reduces to Hooke's Law
as a
function of the length of the band, and show that it reduces to Hooke's Law
![]() in the limit
in the limit ![]() . Find expressions for the coefficient
. Find expressions for the coefficient ![]() and for
the coefficient of thermal expansion at fixed tension in the same limit.
and for
the coefficient of thermal expansion at fixed tension in the same limit.
The coefficient of thermal expansion is negative, showing that the band shrinks when it is warmed. Explain why one might have expected this result without calculation.
[You may use Stirling's approximation
![]() .]
.]
The expression for ![]() is obtained just like that for the two-state
paramagnet in a magnetic field which was question 13 of examples 6.
The tension plays a similar role for a band to the pressure for a gas, so the
relation we want is analogous to
is obtained just like that for the two-state
paramagnet in a magnetic field which was question 13 of examples 6.
The tension plays a similar role for a band to the pressure for a gas, so the
relation we want is analogous to
![]() (see here);
rearranging the fundamental thermodynamic
relation to get
(see here);
rearranging the fundamental thermodynamic
relation to get ![]() on the left hand side, we see that
on the left hand side, we see that
![]() . This
can then be calculated in terms of
. This
can then be calculated in terms of
![]() and
and
![]() ; again see the paramagnet example for
guidence with algebra.
You will need
; again see the paramagnet example for
guidence with algebra.
You will need
![]() for small
for small ![]() . The answers are
. The answers are
![]() and
and
![]() .
.