Arrangements are covered here.
- (a)
- Four dice are rolled. What is the probability of obtaining four sixes?
A six, a five, a four and a three? Two sixes and two fives?
- (b)
- A monkey types eight letters at random on a keyboard of 26 symbols. What is the
probability that all are ``a''? That all of the first eight letters of the alphabet are
present? Five ``a''s and three ``b''s? Three ``a''s, three ``b''s and two ``c''s?
- (c)
- A child distributes eight identical marbles between three different boxes. How many arrangements
are there? (Hint: consider all the possible arrangements
of eight marbles and two partitions in a line, but remember that the partitions are identical, as are the marbles.)
- (d)
- One joule of heat is added reversibly to 1 kg of water at
300 K. What is the increase in entropy of the water? By what factor does the number of
accessible microstates increase?
Hint: first calculate the increase in entropy (the isothermal expression is a very reasonable approximation) then use the connection between entropy and microstates.
- (a)
- Suppose we define the macrostate of a lattice of
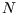 spin-
spin-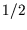 atoms by specifying the number of up-spins
atoms by specifying the number of up-spins 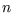 . What is the
statistical weight
. What is the
statistical weight 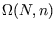 of this macrostate? What is the maximum
value
of this macrostate? What is the maximum
value 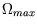 of
of 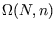 as a function of
as a function of 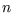 ?
?
- (b)
- Plot
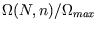 versus
versus 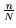 for
for 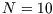 and
and 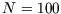 on the same graph. Comment on the form of your
graph.
on the same graph. Comment on the form of your
graph.
(Most calculators will fail to cope with factorials above 69, as the power of ten exceeds 100. For
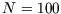 you can use use the most accurate form of Stirling's
approximation,
you can use use the most accurate form of Stirling's
approximation,
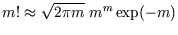 , or you can stick to
, or you can stick to 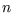 in the range
35 to 65 since
in the range
35 to 65 since
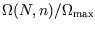 is very small outside that range. Either way you will
still have to do some cancellation by hand and enter large and small terms alternately!)
is very small outside that range. Either way you will
still have to do some cancellation by hand and enter large and small terms alternately!)
- (c)
- Plot the function
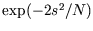 , where
, where 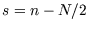 , and
show that it is a good approximation to
, and
show that it is a good approximation to
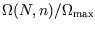 when
when
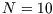 and an excellent one when
and an excellent one when 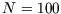 .
.
See here.
![]() ,
, ![]() and
and ![]() can be found from suitable derivatives of the entropy.
can be found from suitable derivatives of the entropy.
where
If the sample is in a magnetic field ![]() which is in the
which is in the ![]() -direction, and
the spins have magnetic moment
-direction, and
the spins have magnetic moment ![]() , show that the internal energy is
, show that the internal energy is
![]() .
.
Using the statistical mechanical
definition of temperature and
show that the internal energy is given in terms of the temperature by
(Hint - first find
This question is covered here.