3.2 The statistical basis of entropy

Take-home message: The increase of entropy can be understood as an evolution from less to more probable configurations

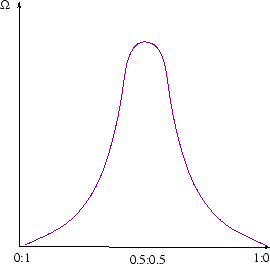
Suppose a system has an extra degree of freedom which isn't specified by fixing the volume and internal energy. For a mixture of two ideal gases, it could be the degree to which they are fully mixed-for example ratio of the concentrations of one species on either side of the box. If the gases started out separated by a partition the concentrations would start at 0:1; the classical law of increase of entropy tells us they will evolve till the ratio reaches 0.5:0.5, and not change thereafter. (See here for a calculation of the entropy change). At the classical level, we don't understand this yet. It is just a law of nature, deduced ultimately from observation.

Statistical physics can explain the spontaneous increase of entropy. There are many more microstates corresponding to the equilibrium configuration (fully mixed) than the non-equilibrium configurations (not fully mixed). The number of microstates as a function of mixing looks something like this, but really much sharper:

If we start at a point of unequal mixing, the configurations which are rather better mixed are more numerous than those which are rather less well mixed. So as interactions cause the system to jump from one microstate to another, it is more likely to end up better mixed. This continues till full mixing is reached, at which point there is no further direction to the changes.

What has this to do with entropy? Classically, the system is evolving from a macrostate of lower entropy to one of higher entropy. Statistically, it is evolving from less probable to more probable macrostates, that is from macrostates corresponding to smaller numbers of microstates to those corresponding to larger numbers of microstates.

So does the number of microstates, $\Omega$, equal the entropy? No, because if we double the size of a system, we have $\Omega^2$, not $2\Omega$, microstates (think of the number of ways of choosing the microstate of each half independently). So $\Omega$ isn't extensive. But $\ln\Omega$ is. So if we make the connection

$\mbox{\LARGE\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle S=k_{\scriptscriptstyle B}\ln\Omega $ }}$

then we can understand both entropy and its increase.

In principle, if the increase of entropy is just a probabilistic thing, it might sometimes decrease. However we will see that for macroscopic systems the odds are so overwhelmingly against an observable decrease that we might as well say it will never happen.

What is $k_{\scriptscriptstyle B}$, Boltzmann's constant? It must be a constant with dimensions of entropy, Joules/Kelvin, and it turns out that the correct numerical correspondence is given by the gas constant $R$ divided by Avogadro's number:

$$k_{\scriptscriptstyle B}=\frac R N_A =1.381\times 10^{-23}\hbox{J\,K$^{-1}$}=8.617\times 10^{-5}\hbox{eV\,K$^{-1}$}$$

Find a simple example of these ideas here.

References

• Mandl 2.3
• Bowley and Sánchez 4.5
• Kittel and Kroemer 1,2