Equilibrium on the checkerboard

Let's consider the checkerboard example again. Imagine starting with a perfectly ordered all-blue board, then choosing a counter at random, tossing it, and replacing it. After repeating this a few times, there are highly likely to be some green counters on the board--the chance of the board remaining blue is only about 1 in $2^n$ after $n$ moves. As time goes on, the number of greens will almost certainly increase--not on every move, but over the course of a few moves. Here is a snapshot of the board taken once every 10 moves. The number of greens is 0, 3, 5, 9, 12, 15, 15, 17, 18.

Here is a graph of the number of greens over 100 and 1000 moves.

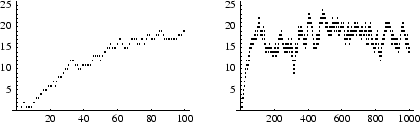
We see that, after the first 100 moves, the system stayed between $18\pm6$ almost all of the time. These fluctuations are quite large in percentage terms, $\pm 33$%, but then it is a very small system--not really macroscopic at all.

If we now look at a larger system, $30\times30$, we see that fluctuations are still visible, but they are much smaller in percentage terms-the number of greens is mostly $450\pm 30$, or $\pm 7$%.

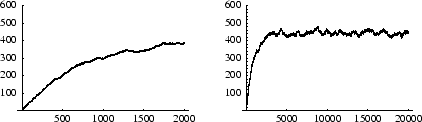
A 25-fold increase in the size of the system has reduced the percentage fluctuations by a factor of 5. We will see later that an $n$-fold increase should indeed reduce the fluctuations by $\sqrt{n}$. We can predict that a system with $10^{23}$ counters--truly macroscopic--would have fluctuations of only about $10^{-10}$%, which would be quite unobservable. The entropy of the system would never appear to decrease.