Microstates

Imagine we have counters, blue on one side and green on the other, and we toss them and place them on a $6\times6$ checkerboard. Full information involves listing the colour at each site: this is the equivalent of a microstate.

Many different patterns are possible, such as the following. Every configuration is equally likely--or unlikely--to occur: There are $\Omega=2^{36}=6.87\times10^{10}$ patterns and the the probability of each is $(1/2)^{36}=1.46\times10^{-11}$. (This satisfies the ``postulate of equal a priori probabilities''.)

Suppose from a distance we only knew how many counters were green and how many blue, without being able to distinguish different arrangements of the same numbers of counters. Then a ``macrostate'' would be characterised simply by the total number of green counters (the rest being blue).

Clearly, most macrostates correspond to many microstates. If the macroscopic description is ``15 green'', the following are a few of the allowed microstates:

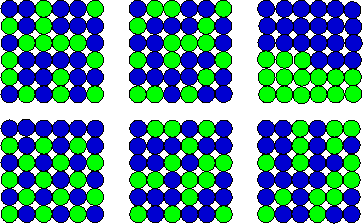
How many are there in total? This is the common problem of splitting a group of $N$ into two smaller groups, of $n$ and $N-n$, without caring about the ordering in each group, and the number of ways of doing it is

$${N!\over n! (N-n)!}$$

Think of counters on squares: there are $N!$ ways of putting $N$ distinguishable counters on $N$ squares. However if $n$ of the counters are green, there are $n!$ ways of arranging the green counters among themselves without changing the pattern, and $(N-n)!$ ways of arranging the blues.
Here, $N=36$ and $n=15$, so the total is $5.59\times 10^9$. For $n=10$ there are only $2.54 \times 10^8$, whereas for $n=18$, there are $9.08\times 10^9$. This is the maximum.

The numbers $N!/ n! (N-n)!$ are called the binomial coefficients (since they enter the binomial expansion) and they are written ${}^NC_n$ or $({N\atop n})$.