What is a spin-
![]() paramagnet? A paramagnet is a substance which can be magnetised by an external magnetic
field, and the magnetisation is aligned with the external field. Unlike a ferromagnet the response is weak and
does not remain if the field is switched off.
paramagnet? A paramagnet is a substance which can be magnetised by an external magnetic
field, and the magnetisation is aligned with the external field. Unlike a ferromagnet the response is weak and
does not remain if the field is switched off.
A crystal of atoms with non-zero spin will act as a paramagnet, as the spins will tend to line up in an external
field. From quantum mechanics we know the spin-projection along the field can only take certain discrete values.
For simplicity we consider spin-
![]() , so that
, so that
![]() .
In an ideal paramagnet, the spins do not feel
one another, but react independently to an external field.
.
In an ideal paramagnet, the spins do not feel
one another, but react independently to an external field.
Thus the ideal paramagnet is a lattice of ![]() sites at each of which the spin points either up or down. Each of these
has a magnetic moment
sites at each of which the spin points either up or down. Each of these
has a magnetic moment ![]() . Only the total magnetic moment is macroscopically measurable, and this is just
the sum of the individual moments. If
. Only the total magnetic moment is macroscopically measurable, and this is just
the sum of the individual moments. If ![]() spins are pointing up and
spins are pointing up and
![]() are pointing down, the total
magnetic moment is
are pointing down, the total
magnetic moment is
However we are going to start with zero external magnetic field so that all states have the same energy. The magnetisation is then an example of an extra degree of freedom not specified by the energy, as discussed in the previous section.
If you haven't already looked at the chequerboard examples, here and
here, do so now. All the pictures carry over if for ``blue'' you read spin-up.
(The chequerboard is 2-D and a crystal is 3-D, but in the absence of interaction the geometry is irrelevant;
all that counts is the total number ![]() of atoms.)
of atoms.)
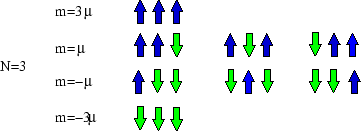
So macrostates are characterised by their magnetic moment (or magnetisation, ![]() ), but microstates by the
list of spins at each site. For
), but microstates by the
list of spins at each site. For ![]() there are four macrostates and nine microstates.
there are four macrostates and nine microstates.
Below we plot ![]() , normalised to 1 at the peak, as a function of
, normalised to 1 at the peak, as a function of ![]() , for different values of
, for different values of ![]() .
.
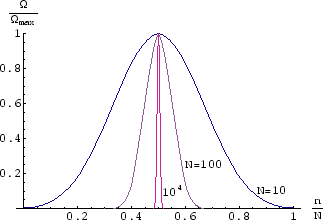
As ![]() gets larger, the function is more and more sharply peaked, and it is more and more likely that in the
absence of an external magnetic field there will be equal numbers of up and down spins, giving zero magnetisation.
gets larger, the function is more and more sharply peaked, and it is more and more likely that in the
absence of an external magnetic field there will be equal numbers of up and down spins, giving zero magnetisation.
For large ![]() , the curve is very well approximated by a Gaussian,
, the curve is very well approximated by a Gaussian,
Since the probabilities of various sizes of fluctuations from the mean in a Gaussian are known, we can show
that in a macroscopic system, ![]() deviations are vanishingly unlikely. Even they would be
undetectable, so the macroscopic magnetisation is very well defined indeed.
deviations are vanishingly unlikely. Even they would be
undetectable, so the macroscopic magnetisation is very well defined indeed.
References