3.4 From entropy to temperature

Take-home message: From the entropy, we can calculate all the usual functions of state of a system

In the last section we deduced the existence of entropy, and the fact that at equilibrium the entropy is a maximum, from statistical arguments. Now we would like to know if we could go further and, even if we knew no classical thermodynamics, deduce the existence of temperature, pressure and chemical potential.

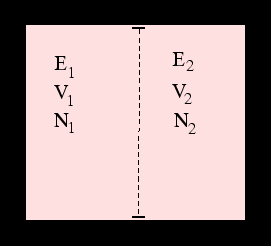
By considering two systems in contact with one another we can indeed deduce the existence of properties which determine whether they are in thermal, mechanical and diffusive equilibrium even if we knew no classical thermodynamics: these are the three partial derivatives of the entropy with respect to energy, volume and particle number.

Clearly these are related to the usual concepts of temperature, pressure and chemical potential. The correct relations are the ones which reproduce the fundamental thermodynamic relation

$${\rm d}S= {1\over T} {\rm d}E +{P\over T}{\rm d}V -{\mu\over T}{\rm d}N,$$

namely

$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle\left({\p... ...e\left({\partial S\over\partial N}\right)_{\!\scriptstyle E,V}=-{\mu\over T}$}}$

Details of the derivation are given here.

As an example, these ideas are applied to the paramagnet here. We can have our first go at the ideal gas now, too; see here.

References

• Mandl 2.4
• (Bowley and Sánchez 2.9)