The ideal gas, first attempt

To do the ideal gas properly we need to know the quantum states of particles in a box. We learned this in PC210 last semester, so we will be able to tackle it properly later. However with much less work we can at least discover how the entropy depends on volume at fixed particle number and energy.

Consider an isolated system of $N$ atoms in a box of volume $V$. Imagine the box subdivided into many tiny cells of volume $\Delta V$, so that there are $V/\Delta V$ cells in all (this number should be much greater than $N$). Now each atom can be in any cell, so there are $V/\Delta V$ microstates for each atom, and $(V/\Delta V)^N$ microstates for the gas as a whole. Thus

$$S=N k_{\scriptscriptstyle B}\ln\left({V\over\Delta V}\right)$$

and

$$\begin{eqnarray*} {P\over T}\!\!\!&=&\!\!\!\left({\partial S\over\partial V}\rig... ...ghtarrow PV\!\!\!&=&\!\!\!N k_{\scriptscriptstyle B}T\nonumber \end{eqnarray*}$$

So we have derived the ideal gas equation!

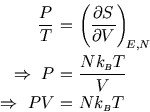
A problem with this expression for the entropy is that it depends on the size $\Delta V$ of the imaginary cells into which we subdivided our box. This is clearly unsatisfactory (though at least entropy changes are independent of it), but classical physics can't do any better. Quantum physics can though! If you want to jump ahead to see the full expression (called the Sackur-Tetrode equation) see here.