The isolated spin-half paramagnet in a magnetic field

We can apply these to the spin- ${\textstyle \frac 1 2}$ paramagnet in a magnetic field. There is just one difference: we can't derive pressure in this case, because the work is magnetic and not mechanical. Instead of $-P{\rm d}V$ we have $-m {\rm d}B$ in the fundamental thermodynamic relation, so we have an expression for $m$ instead of $P$:

$${m\over T}=\left({\partial S\over\partial B}\right)_{\!\scriptstyle E,N}$$

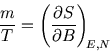
Now for an isolated system the energy is fixed, and therefore so is the number of up spins: $E=-\mu B(n_\uparrow -n_\downarrow )=\mu B(N-2n_\uparrow )$ (note $\mu$ is now the magnetic moment!) Then we have

$$S=k_{\scriptscriptstyle B}\ln\Omega(E,B)=k_{\scriptscriptstyle B}\ln\left({N!\over n_\uparrow ! (N-n_\uparrow )!}\right)$$

with $n_\uparrow \approx {\textstyle \frac 1 2}(N-E/\mu B)$.

For large numbers of spins, we can use Stirling's approximation:

$$\ln n!=n\ln n-n$$

giving

$$S=k_{\scriptscriptstyle B}\left(N \ln N - n_\uparrow \ln n_\uparrow -(N-n_\uparrow )\ln(N-n_\uparrow )\right).$$

(Note that $S$ is maximum, $S=Nk_{\scriptscriptstyle B}\ln 2$, when $n_\uparrow =n_\downarrow =N/2$, the point of maximum disorder. This is the expected value, as at this point $\Omega=2^N$)

So

$$\begin{eqnarray*} {1\over T}\!\!\!&=&\!\!\!\left({\partial S\over\partial E}\rig... ...2\mu B}\ln\left({n_\uparrow \over n_\downarrow }\right)\nonumber \end{eqnarray*}$$

There will always be more spins aligned with the field than against it, so $T$ is positive.

Differentiating the entropy with respect to $B$ instead, and using the above result for $T$, we get an expression for $m$:

$$\begin{eqnarray*} {m\over T}\!\!\!&=&\!\!\!-{k_{\scriptscriptstyle B}\over 2\mu ... ...\downarrow }\right)\nonumber \quad \Rightarrow m = -{E\over B} \end{eqnarray*}$$

We knew that of course, but it's good that it works.