




Next: The isolated spin-half paramagnet in a
Previous: 3.4 From entropy to temperature
Deriving temperature etc
We can derive the ideas of temperature, pressure and chemical potential from the entropy.
Consider a system divided in two by a wall which can move, and through which energy and particles can pass.
The equilibrium division of the space into two volumes 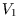 and
and 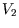 , with energy and particle number similarly
divided, will be the one which corresponds to the maximum number of microstates, and hence to the maximum
entropy. If we consider heat flow only,
, with energy and particle number similarly
divided, will be the one which corresponds to the maximum number of microstates, and hence to the maximum
entropy. If we consider heat flow only,
.
But the microstates of each half can be counted independently, so the entropies add:
and also, since the total energy is conserved,
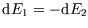 .
So
.
So
and the entropy will be maximised when a small energy flow no longer changes the entropy:
So we deduce there is some property of bodies which governs heat flow; this is clearly related to temperature.
By considering volume changes and particle flow we discover two more properties which are clearly related to
pressure and chemical potential. To discover the relation we would have to calculate them for some system
and see how they compared with the temperature, pressure etc of classical thermodynamics. However the following
assignments clearly work:
since they give
which is the fundamental thermodynamic relation rearranged.





Next: The isolated spin-half paramagnet in a
Previous: 3.4 From entropy to temperature
Judith McGovern
2004-03-17
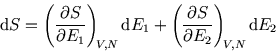
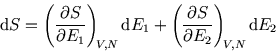
![\begin{displaymath}
{\rm d}S=\left[\left({\partial S_1\over\partial E_1}\right)_...
...partial E_2}\right)_{\!\scriptstyle V_2,N_2}\right] {\rm d}E_1
\end{displaymath}](img485.gif)
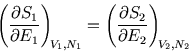
![$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \
$\displaystyle\left({\p...
...e\left({\partial S\over\partial N}\right)_{\!\scriptstyle E,V}=-{\mu\over T}$}}$](img480.gif)