1.4 Work

Take home-message: the expressions for reversible work for various systems

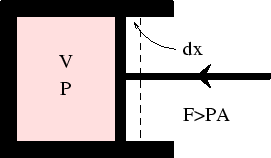
First, we consider the work done in compressing a fluid (hydrodynamic system).

In any real case, compression requires the applied force to be greater than the internal pressure times the area of the piston: $F>PA$. The work done in moving the piston though ${\rm d}x$ is

$${}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}W= F {\rm d}x = - \frac F A {\rm d}V > - P {\rm d}V$$

Note this is positive for compression, because ${\rm d}V$ is negative.

If there is no friction, and the compression is done extremely slowly, the applied force will only be barely greater than $PA$. In that case the process is reversible, and the inequality will become an equality:

$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle {}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}W^{\rm rev}= - P {\rm d}V$ }}$

See here to revisit a previous example.

Similarly to reversibly stretch a wire of tension $\Gamma$ (that's a capital gamma) by ${\rm d}l$ requires

$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle {}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}W^{\rm rev}= \Gamma {\rm d}l$ }}$

and to increase the area of a film of surface tension $\gamma$ by ${\rm d}A$ requires

$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle {}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}W^{\rm rev}= \gamma {\rm d}A$ }}$

Note in the last two cases the sign is different from the first; that's because it takes work to stretch a wire or a soap film (${\rm d}l$ or ${\rm d}A$ positive) but to compress a gas (${\rm d}V$ negative).

Lastly, to reversibly increase the magnetic field $B$ imposed upon a paramagnetic sample requires

$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle {}\rai... ...}W^{\rm rev}= -{\bf m}\cdot{\rm d}{\bf B} =-V{\bf M}\cdot{\rm d}{\bf B} $ }}$

where M is the magnetisation per unit volume, and m is the total magnetic moment of the sample.

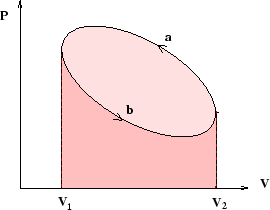
If reversible processes are represented by lines on a plot of pressure against volume (or tension against length, or...), then the magnitude of the work done is equal to the area under the line. Cycles are closed loops as in the picture above, and the magnitude of the work done is equal to the area of the loop (that is, the difference between the areas under the two lines).

Test yourself with this example. More can be found on the tutorial sheet.

References

• Mandl 1.3-4
• Bowley and Sánchez 1.6
• Adkins 3.5
• Zemansky 3

(Be warned: Adkins and Zemansky use a different definition of magnetic work, which is less convenient for statistical thermodynamics.)