Work during free and reversible expansions

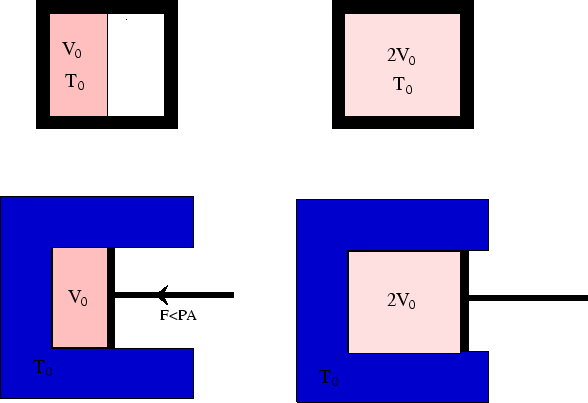
In this example (see here) we saw that the work done by an ideal gas during isothermal expansion could be zero (for free expansion into a vacuum) or non-zero (for expansion against a force). In the first case the process is non-reversible. We now see that in the second case, if the process is reversible, the work done by the gas on the surroundings will be

$$-W^{\rm rev}=\int P{\rm d}V =\int_{V_1}^{V_2} {nR T\over V}{... ... =nR T\int _{V_1}^{V_2}{{\rm d}V\over V}=nR T\ln{V_2\over V_1}$$

where we used the ideal gas law $P=nRT/V$, and we could take $T$ out of the integral because the process is isothermal.

The reversible process extracts the maximum work from the gas, as no work is lost overcoming friction or creating sound waves. In a non-reversible process, these are both mechanisms which convert energy which could have gone into work into internal energy of the gas instead, and so the gas will need to extract less heat from the surroundings. Thus $Q+W=0$ will still hold.