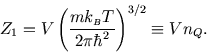
We are now reaching the most important test of statistical physics: the ideal gas. For the moment we assume it is monatomic; the extra work for a diatomic gas is minimal.
Remember the one-particle translational partition function, at any attainable
temperature, is
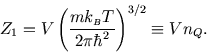
But if we follow this through and calculate the Helmholtz free energy and the entropy, we find that the results
do not make sense: specifically, if one has double the number of particles, in double the volume, the entropy and
the Helmholtz free energy, like the energy, should double. These are
extensive variables.
But if we go ahead and calculate based on ![]() , we do not get extensive results, but terms like
, we do not get extensive results, but terms like ![]() .
.
However we shouldn't have expected ![]() to work, because the derivation
was based on the idea that every one
of the
to work, because the derivation
was based on the idea that every one
of the ![]() particles was distinguishable. But at a completely fundamental level, every molecule is
exactly the same as every other molecule of the same substance.
particles was distinguishable. But at a completely fundamental level, every molecule is
exactly the same as every other molecule of the same substance.
The exact form of ![]() in this case has no compact form. But there is an approximation which becomes exact
in the limit of low number densities
in this case has no compact form. But there is an approximation which becomes exact
in the limit of low number densities ![]() : specifically
: specifically ![]() where
where
![]() is
the ``quantum concentration'' and is a measure of the number of
energy levels available. It is also proportial to the inverse of cube of the thermal de Broglie wavelength (the wavelength of a particle of energy of order
is
the ``quantum concentration'' and is a measure of the number of
energy levels available. It is also proportial to the inverse of cube of the thermal de Broglie wavelength (the wavelength of a particle of energy of order
![]() ).
The significance of this limit is
that it is very unlikely that any two atoms are in the same energy level. This is called the classical limit.
).
The significance of this limit is
that it is very unlikely that any two atoms are in the same energy level. This is called the classical limit.
![$\mbox{\LARGE\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \
$\displaystyle Z_N={(Z_1)^N\over N!}$ }}$](img730.gif)
Now, using Stirling's approximation
![]() , we find
, we find
![\begin{eqnarray*}
\left\langle F \right\rangle \!\!\!&=&\!\!\!-k_{\scriptscripts...
...iptscriptstyle B}T \left[\ln\left({ n\over n_Q}\right)-1\right].
\end{eqnarray*}](img732.gif)
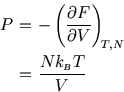
The expression for ![]() is clearly experimentally verifiable: it is the ideal gas law. That's good, but we
expected to get that. More interestingly the Sackur-Tetrode equation for
is clearly experimentally verifiable: it is the ideal gas law. That's good, but we
expected to get that. More interestingly the Sackur-Tetrode equation for ![]() can also be checked. First, if
we unpick the dependence on
can also be checked. First, if
we unpick the dependence on ![]() and
and ![]() , we get
, we get
Finally, we include vibrations and rotations as well as translations: since the one-particle energies are
independent and add,
![]() , the partition
functions multiply:
, the partition
functions multiply:
![]() (the argument is like that for the
(the argument is like that for the ![]() -particle
partition function for distinguishable particles and is given in more detail here) and so
-particle
partition function for distinguishable particles and is given in more detail here) and so
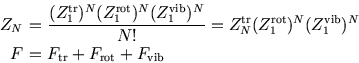
References