




Next: 4.8 The Equipartition Theorem
Previous: 4.6 Vibrational and rotational energy of
4.7 Translational energy of a molecule in an ideal gas
This example is rather more complicated than the preceding ones, but the result is simple and powerful.
The non-interacting atoms of the gas are in a cuboidal box of side lengths 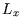 ,
, 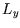 and
and 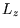 , and volume
, and volume
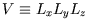 . The sides of the box are impenetrable, so the wavefunction
. The sides of the box are impenetrable, so the wavefunction 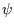 must vanish there,
but inside the box the atom is free and so
must vanish there,
but inside the box the atom is free and so 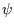 satisfies the free Schrödinger equation
satisfies the free Schrödinger equation
The equation, and the boundary conditions, are satisfied by
with 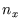 ,
, 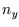 and
and 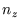 integers greater than zero.
The corresponding energy is
integers greater than zero.
The corresponding energy is
where
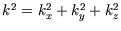 and
and
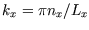 etc.
So the one-particle partition function is
etc.
So the one-particle partition function is
In general this cannot be further simplified. However there can be
simplifications if
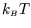 is much greater than the spacing between the energy levels,
as we saw in the rotational case. For a volume of 1 litre, that
spacing is of order
is much greater than the spacing between the energy levels,
as we saw in the rotational case. For a volume of 1 litre, that
spacing is of order
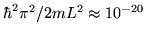 eV--truly tiny. Even at the lowest temperatures ever reached, we
are in the high-temperature regime! Thus we can replace the sum over levels by an integral. We choose
eV--truly tiny. Even at the lowest temperatures ever reached, we
are in the high-temperature regime! Thus we can replace the sum over levels by an integral. We choose
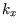 ,
, 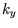 and
and 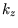 as the variables, and replace
as the variables, and replace
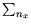 with
with
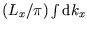 , giving
, giving
The factor of 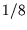 in the penultimate line comes from the fact that we only integrated over positive values of
in the penultimate line comes from the fact that we only integrated over positive values of
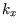 etc, that is over the positive octant of
etc, that is over the positive octant of 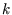 -space.
-space.
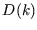 is called the ``density of states'' in
is called the ``density of states'' in 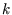 -space;
-space; 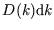 is the number of states within range of
is the number of states within range of
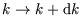 . See here for more on this concept.
. See here for more on this concept.
This section only depended on the fact that the energy is independent of the direction of 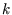 . Now we use
the actual form of
. Now we use
the actual form of
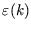 to complete the calculation:
to complete the calculation:
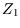 is a pure number, so ``
is a pure number, so ``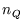 '' must have dimensions of
'' must have dimensions of 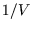 like a number density; it is called the
quantum concentration and is temperature-dependent.
From
like a number density; it is called the
quantum concentration and is temperature-dependent.
From 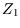 we can obtain the average single particle energy:
we can obtain the average single particle energy:
as we should have expected.
References
- Mandl 7.1-4, Appendix B
- Bowley and Sánchez 5.9,7.2
- Kittel and Kroemer 3
Subsections





Next: 4.8 The Equipartition Theorem
Previous: 4.6 Vibrational and rotational energy of
Judith McGovern
2004-03-17
![]() ,
, ![]() and
and ![]() , and volume
, and volume
![]() . The sides of the box are impenetrable, so the wavefunction
. The sides of the box are impenetrable, so the wavefunction ![]() must vanish there,
but inside the box the atom is free and so
must vanish there,
but inside the box the atom is free and so ![]() satisfies the free Schrödinger equation
satisfies the free Schrödinger equation
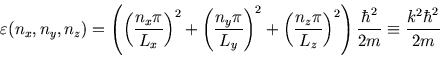
![]() . Now we use
the actual form of
. Now we use
the actual form of
![]() to complete the calculation:
to complete the calculation: