




Previous: 4.7 Translational energy of a molecule
The Density of States
Going through the algebra to calculate the translational partition function we turned a sum over the integers
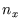 ,
, 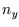 and
and 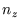 which count the number of half wavelengths along the three sides, to an integral over
which count the number of half wavelengths along the three sides, to an integral over
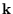 . Since the energy depends only on
. Since the energy depends only on 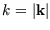 , we could do the integral over the direction of
, we could do the integral over the direction of 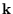 leaving only the integral over
leaving only the integral over 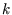 ; in this process we collected a number of factors and called them the
density of state:
; in this process we collected a number of factors and called them the
density of state:
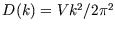 , so that
, so that
We see that 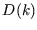 is acting as a ``degeneracy factor'', which we first met in the context of the
rotor. If there is more than one energy level with the same energy, and we replace
the sum over individual states with a sum over allowed energies, we need to include a factor in front of the
Boltzmann factor for degenerate levels so that they are counted often enough.
is acting as a ``degeneracy factor'', which we first met in the context of the
rotor. If there is more than one energy level with the same energy, and we replace
the sum over individual states with a sum over allowed energies, we need to include a factor in front of the
Boltzmann factor for degenerate levels so that they are counted often enough.
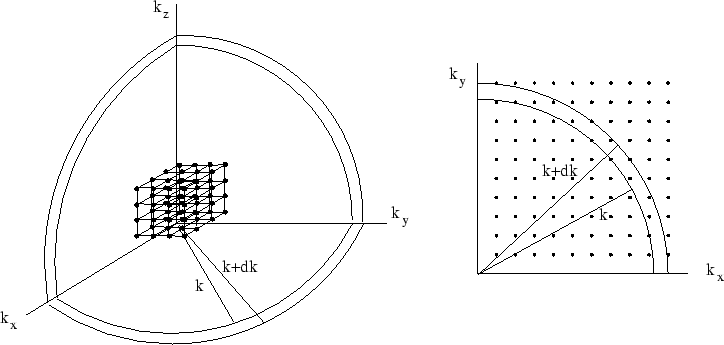
The picture above shows a graphical representation of the allowed states in 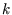 -space. Since
-space. Since
with 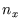 etc positive, the allowed values of k form a three-dimensional lattice.
The density of states is the number of states within an infinitesimal range of
etc positive, the allowed values of k form a three-dimensional lattice.
The density of states is the number of states within an infinitesimal range of 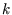 , and hence of energy.
This is just the volume of an octant of a spherical shell,
, and hence of energy.
This is just the volume of an octant of a spherical shell,
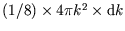 , divided by
the volume of
, divided by
the volume of 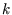 -space per state,
-space per state, 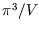 , giving
, giving





Previous: 4.7 Translational energy of a molecule
Judith McGovern
2004-03-17
![]() -space. Since
-space. Since