4.8 The Equipartition Theorem

Take-home message: The classical theory of equipartition holds in the high-temperature limit

The results for vibrational, rotational and translational energies demonstrate that, at high enough temperatures, the law of equipartition of energy holds: each quadratic term in the classical expression for the energy contributes ${\textstyle \frac 1 2}k_{\scriptscriptstyle B}T$ to the average energy and ${\textstyle \frac 1 2}k_{\scriptscriptstyle B}$ to the heat capacity. The oscillator has quadratic kinetic and potential terms:

$$E_{\rm vib}={\textstyle \frac 1 2}m \dot x^2+{\textstyle \fr... ...^2 x^2 \qquad\hbox{2 d.o.f, $E\to k_{\scriptscriptstyle B}T$}.$$

The rotor has two perpendicular axes about which it can rotate; each with a quadratic kinetic energy (rotations about the axis have no effect in quantum mechanics; classically the moment of inertia is tiny):

$$E_{\rm rot}={\textstyle \frac 1 2}{\cal I} \omega_1^2+{\text... ...ega_2^2\qquad\hbox{2 d.o.f, $E\to k_{\scriptscriptstyle B}T$}.$$

The translational kinetic energy has three terms for the three dimensions of space:

$$E_{\rm tr}={\textstyle \frac 1 2}m \dot x^2+{\textstyle \fra... ...quad\hbox{3 d.o.f, $E\to \frac 3 2k_{\scriptscriptstyle B}T$}.$$

Now we understand what governs ``high enough'': $k_{\scriptscriptstyle B}T$ has to be much greater than the spacing between the quantum energy levels. If this is not satisfied, the heat capacity will be reduced, dropping to zero at low temperatures. The corresponding degree of freedom is said to be frozen out; this is the situation for the vibrational degrees of freedom at room temperature.

Here is an idealised graph of the heat capacity of hydrogen with temperature, (©P. Eyland, University of New South Wales)

As the moment of inertia for $\rm H_2$ is small, the temperature by which equipartition holds for rotational modes is actually quite high. Bowley and Sánchez have a graph taken from data (Fig. 5.8).

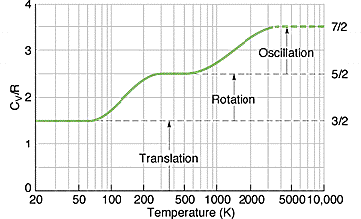
We can predict the specific heat of other substances based on equipartition, simply by counting the degrees of freedom. For a solid, we expect the molar heat capacity to be $3RT$ since each atom is free to vibrate in three directions. This is the law of Dulong and Petit, and it works well for a variety of solids at room temperature. (More details here.)

Equipartition does not hold, even at high temperatures, if the energy is not quadratic. For instance the gravitational potential energy is linear in height, and the average potential energy of a molecule in an isothermal atmosphere is $k_{\scriptscriptstyle B}T$, not ${\textstyle \frac 1 2}k_{\scriptscriptstyle B}T$.

Similarly the kinetic energy of a highly relativistic particle is given by the non-quadratic $c\sqrt{p_x^2+p_y^2+p_z^2} (=\hbar c k)$, not by the quadratic $(p_x^2+p_y^2+p_z^2)/2m$, and the average kinetic energy is $3k_{\scriptscriptstyle B}T$, not $\frac 3 2 k_{\scriptscriptstyle B}T$.

References

• Mandl 7.9
• Bowley and Sánchez 5.14
• (Kittel and Kroemer 3)