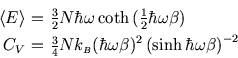Previous: 4.8 The Equipartition Theorem
The heat capacity of a crystal
Based on equipartition, we expect the molar heat capacity for a solid to be 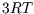 since each atom is free to
vibrate
in three directions. This is the law of Dulong and Petit, and it works well for a variety of solids at
room temperature. It is reproduced, as might be expected, by the Einstein model for a crystal which considers
each atom linked to its neighbours by six springs (
since each atom is free to
vibrate
in three directions. This is the law of Dulong and Petit, and it works well for a variety of solids at
room temperature. It is reproduced, as might be expected, by the Einstein model for a crystal which considers
each atom linked to its neighbours by six springs (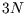 in total)--the algebra is just like that of the
vibrations of a diatomic molecule giving
in total)--the algebra is just like that of the
vibrations of a diatomic molecule giving
At low temperature (
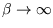 ) the energy tends to
) the energy tends to
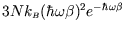 .
Although this tends to zero, it does not agree with the observed low
temperature behaviour, which is proportional to
.
Although this tends to zero, it does not agree with the observed low
temperature behaviour, which is proportional to 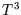 . More sophisticated models, such as that of Debye,
allow for collective vibrations of many atoms which have
much lower frequency, and hence contribute to the internal energy and heat capacity at much lower temperatures.
. More sophisticated models, such as that of Debye,
allow for collective vibrations of many atoms which have
much lower frequency, and hence contribute to the internal energy and heat capacity at much lower temperatures.





Previous: 4.8 The Equipartition Theorem
Judith McGovern
2004-03-17
![]() since each atom is free to
vibrate
in three directions. This is the law of Dulong and Petit, and it works well for a variety of solids at
room temperature. It is reproduced, as might be expected, by the Einstein model for a crystal which considers
each atom linked to its neighbours by six springs (
since each atom is free to
vibrate
in three directions. This is the law of Dulong and Petit, and it works well for a variety of solids at
room temperature. It is reproduced, as might be expected, by the Einstein model for a crystal which considers
each atom linked to its neighbours by six springs (![]() in total)--the algebra is just like that of the
vibrations of a diatomic molecule giving
in total)--the algebra is just like that of the
vibrations of a diatomic molecule giving