




Next: Details of the paramagnet calculation
Previous: 4.4 The paramagnet at fixed temperature
The N-particle partition function for distinguishable particles
Let's start with two spins. There are four states of the whole system,
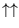 with energy
with energy 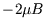 ,
,
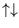 and
and
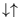 , both with energy zero, and
, both with energy zero, and
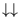 with energy
with energy 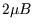 . Thus the two-particle partition function is
. Thus the two-particle partition function is
In general, for 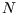 particles, the energies range through
particles, the energies range through
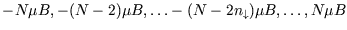 with there being
with there being
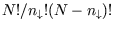 separate states with
separate states with 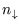 down-spins. So
down-spins. So
The treatment for a system with more than two single-particle states is covered here.
There is a caveat, which can be ignored on first reading. The argument says that there are a number of different
states with the same number of down spins. Since the spins are arranged on a lattice, this is correct; every
spin can be distinguished from every other spin by its position. When we go on to consider a gas, however, this
is no longer so, and the relation between 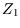 and
and 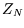 changes. The treatment for indistinguishable particles
is here.
changes. The treatment for indistinguishable particles
is here.





Next: Details of the paramagnet calculation
Previous: 4.4 The paramagnet at fixed temperature
Judith McGovern
2004-03-17
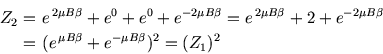
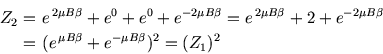
![]() and
and ![]() changes. The treatment for indistinguishable particles
is here.
changes. The treatment for indistinguishable particles
is here.