First, recap previous sections on the isolated spin-
![]() paramagnet at zero and
non-zero magnetic field.
paramagnet at zero and
non-zero magnetic field.
The ideal paramagnet is a lattice of ![]() sites at each of which the spin points either up or down. Each of these
has a magnetic moment
sites at each of which the spin points either up or down. Each of these
has a magnetic moment ![]() .
In an external field, these two states will have different energy; spin-up has energy
.
In an external field, these two states will have different energy; spin-up has energy ![]() , and
spin-down,
, and
spin-down, ![]() . As we saw previously the partition function for a single atom
is therefore
. As we saw previously the partition function for a single atom
is therefore
Since the atoms are non-interacting, the total energy and magnetisation of the system are just ![]() times the
average energy and magnetisation of a single spin. The energy is
times the
average energy and magnetisation of a single spin. The energy is
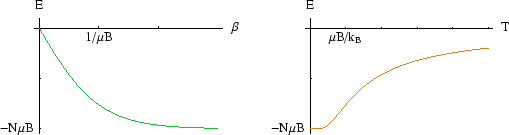
At low ![]() , all the spins are aligned with the field and the energy per spin is close to
, all the spins are aligned with the field and the energy per spin is close to ![]() . However
as
. However
as ![]() increases, thermal fluctuations start to flip some of the spins; this is noticeable when
increases, thermal fluctuations start to flip some of the spins; this is noticeable when
![]() is of the
order of
is of the
order of ![]() . As
. As ![]() gets very large, the energy tends to zero as the number of up and down spins become
more nearly equal. Remember,
gets very large, the energy tends to zero as the number of up and down spins become
more nearly equal. Remember,
![]() , so it never exceeds one.
, so it never exceeds one.
We can also calculate the heat capacity :
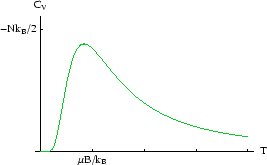
We see that the heat capacity tends to zero both at high and low ![]() . At low
. At low ![]() the heat capacity is small
because
the heat capacity is small
because
![]() is much smaller than the energy gap
is much smaller than the energy gap ![]() , so thermal fluctuations which flip spins are
rare and it is hard for the system to absorb heat. This behaviour is universal; quantisation means that there
is always a minimum excitation energy of a system and if the temperature is low enough, the system can no longer
absorb heat.
, so thermal fluctuations which flip spins are
rare and it is hard for the system to absorb heat. This behaviour is universal; quantisation means that there
is always a minimum excitation energy of a system and if the temperature is low enough, the system can no longer
absorb heat.
The high-![]() behaviour arises because the number of down-spins never exceeds the number of up-spins, and the energy
has a maximum of zero.
As the temperature gets very high, that limit is close to being reached, and raising the temperature
still further makes very little difference.
This behaviour is not universal, but only occurs where there is a finite number of energy levels (here, there
are only two). Most systems have an infinite tower of energy levels, there is no maximum energy and the heat capacity
does not fall off.
behaviour arises because the number of down-spins never exceeds the number of up-spins, and the energy
has a maximum of zero.
As the temperature gets very high, that limit is close to being reached, and raising the temperature
still further makes very little difference.
This behaviour is not universal, but only occurs where there is a finite number of energy levels (here, there
are only two). Most systems have an infinite tower of energy levels, there is no maximum energy and the heat capacity
does not fall off.
Up to now we've cheated a bit, (though the results are correct,) in that we didn't calculate the partition
function for the whole system, only for a single spin. It is easy to show however that the partition
function for ![]() non-interacting spins on a lattice is
non-interacting spins on a lattice is
![$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \
$\displaystyle Z_N=(Z_1)^N$ }}$](img578.gif)
Below we plot ![]() and
and ![]() against temperature for several different external fields.
(For details of the algebra behind the plots see here.)
against temperature for several different external fields.
(For details of the algebra behind the plots see here.)
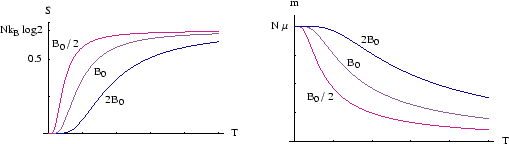
The stronger the field, the higher the temperature has to be before the spins start to be appreciably disordered.
At high temperatures the spins are nearly as likely to be up as down; the magnetisation falls to zero
and the entropy reaches a maximum. The entropy of this
state is
![]() , as we have already seen.
, as we have already seen.
References