4.1 The Boltzmann Distribution

Take-home message: The form of the Boltzmann distribution!

If a system is in contact with a heat bath at temperature $T$, the probability that it is in the $i$th microstate, with energy $\varepsilon_i$, is given by the Boltzmann distribution:

$\mbox{\LARGE\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle p_i={e^{-\varepsilon_i/k_{\scriptscriptstyle B}T} \over Z}$ }}$

The normalisation constant $Z$ is found by saying that the probability that the system is in some microstate is one: $\sum_j p_j =1$, so

$$Z=\sum_j e^{-\varepsilon_j/k_{\scriptscriptstyle B}T}$$

The details of the derivation are here. In outline, we consider the system $S$ and heat reservoir $R$ together as a larger, isolated system with a total energy which is fixed but which can be differently distributed between its two parts. If we specify the microstate (and energy) of $S$, the probability of this depends of the number of microstates of the reservoir with the remaining energy. This decreases with decreasing reservoir energy in just the way given by the Boltzmann distribution.

For an ideal gas or paramagnet, where interactions between atoms can be ignored, any particle can be considered as the system $S$ and all the others form the reservoir $R$. In that case the Boltzmann distribution holds for the state of an individual atom (hence typical first-year applications like the variation of pressure with height in the atmosphere, and the distribution of velocities of atoms in a gas).

For the spin- ${\textstyle \frac 1 2}$ paramagnet in a magnetic field $B$ there only are two energy states; $\varepsilon_\uparrow=-\mu B$ and $\varepsilon_\downarrow=\mu B$. So

$$\begin{eqnarray*} p_\uparrow \!\!\!&=&\!\!\!{e^{ \mu B/ k_{\scriptscriptstyle B... ...k_{\scriptscriptstyle B}T}+e^{-\mu B/ k_{\scriptscriptstyle B}T} \end{eqnarray*}$$

(The label on $Z_1$ refers to the fact that we are talking about the state of a single particle.)

In the whole system of $N$ atoms, the number of up-spins on average will be $\left\langle n \right\rangle _\uparrow =N p_\uparrow$, so we have

$$\left\langle n_\downarrow\over n_\uparrow \right\rangle =e^{-2\mu B/ k_{\scriptscriptstyle B}T}$$

This is exactly consistent with the expression we found for the temperature of the isolated system with a fixed number of up-spins (and hence energy).

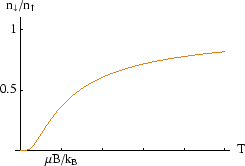
Note that in thermal equilibrium, the average number of particles in the higher energy state is always less than the number in the lower energy state. As the temperature tends to infinity the ratio approaches, but never exceeds, one.

References

• Mandl 2.5
• (Bowley and Sánchez 5.1)
• Kittel and Kroemer 3