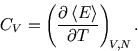Next: 4.3 Entropy, Helmholtz Free Energy and
Previous: 4.1 The Boltzmann Distribution
4.2 The Partition Function
Take-home message: Far from being an uninteresting normalisation constant, 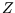 is the key to
calculating all macroscopic properties of the system!
is the key to
calculating all macroscopic properties of the system!
The normalisation constant in the Boltzmann distribution is also called the partition function:
where the sum is over all the microstates of the system.
How can a constant be a function? Well for a given system and reservoir, that is fixed temperature, particle number,
volume or magnetic field (as appropriate), 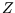 is a constant. But if the temperature etc are allowed to vary,
then
is a constant. But if the temperature etc are allowed to vary,
then 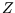 is a function of them:
is a function of them: 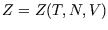 or
or 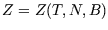 . (The dependence on
. (The dependence on 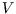 or
or 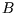 comes through the
energies of the microstates
comes through the
energies of the microstates 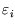 )
)
Why are we emphasising this? Because if we know 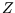 , we can calculate all macroscopic properties of the
system - energy, pressure, magnetisation, entropy...
, we can calculate all macroscopic properties of the
system - energy, pressure, magnetisation, entropy...
For instance the average energy
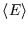 (actually an
ensemble average) is
(actually an
ensemble average) is
The top line is like the bottom line (the partition function) except that each term is multiplied by 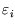 .
We can get the top line from the bottom by differentiating by ``
.
We can get the top line from the bottom by differentiating by ``
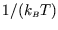 ''. This is a bit awkward, so we
introduce a new symbol
''. This is a bit awkward, so we
introduce a new symbol
giving
or
(where--contrary to the strict instructions given earlier--we will take it for granted that it is particle number
and volume or magnetic field constant that we are holding constant.)
From the energy we can find the heat capacity:
We have found the average energy, but there will be fluctuations as heat is randomly exchanged between the
system and the heat bath. These are given by
It can be shown that 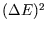 is related to the heat capacity,
is related to the heat capacity,
For a normal macroscopic system the average energy is of the order of
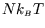 and the heat capacity is
of the order of
and the heat capacity is
of the order of
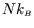 . Thus
. Thus
For a system of 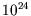 atoms,
atoms,
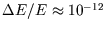 and so fluctuations are unobservable.
There is no practical difference between and isolated system of energy
and so fluctuations are unobservable.
There is no practical difference between and isolated system of energy 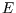 and one in contact with a heat bath at
the same temperature.
and one in contact with a heat bath at
the same temperature.
References
- Mandl 2.5
- Bowley and Sánchez 5.2
- Kittel and Kroemer 3
Subsections





Next: 4.3 Entropy, Helmholtz Free Energy and
Previous: 4.1 The Boltzmann Distribution
Judith McGovern
2004-03-17
![$\mbox{\LARGE\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \
$\displaystyle Z=\sum_j e^{-\varepsilon_j/k_{\scriptscriptstyle B}T}$ }}$](img531.gif)
![$\mbox{\LARGE\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \
$\displaystyle Z=\sum_j e^{-\varepsilon_j/k_{\scriptscriptstyle B}T}$ }}$](img531.gif)
![]() is a constant. But if the temperature etc are allowed to vary,
then
is a constant. But if the temperature etc are allowed to vary,
then ![]() is a function of them:
is a function of them: ![]() or
or ![]() . (The dependence on
. (The dependence on ![]() or
or ![]() comes through the
energies of the microstates
comes through the
energies of the microstates ![]() )
)
![]() , we can calculate all macroscopic properties of the
system - energy, pressure, magnetisation, entropy...
, we can calculate all macroscopic properties of the
system - energy, pressure, magnetisation, entropy...
![]() (actually an
ensemble average) is
(actually an
ensemble average) is
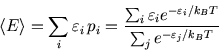
![$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \
$\displaystyle E=-{\partial \ln Z\over \partial \beta}$ }}$](img539.gif)