Fluctuations

To derive $(\Delta E)^2=(k_{\scriptscriptstyle B}T)^2{C_V /k_{\scriptscriptstyle B}}$ the following intermediate steps are useful:

$$\left\langle E^2 \right\rangle = {1\over Z}\left({\partial^2 Z \over \partial \beta^2}\right)_{\scriptscriptstyle N,V}$$

(should be obvious by analogy with the corresponding expression for $\left\langle E \right\rangle$) and hence

$$(\Delta E)^2={\partial^2 \ln Z\over \partial \beta^2}= -{\pa... ...ight\rangle \over \partial T}=k_{\scriptscriptstyle B}T^2 C_V.$$

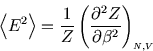
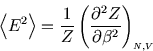
In the main text we said that for ``normal'' macroscopic systems the fluctuations were unobservable. There are exceptions. Near a critical point--where the distinction between two phases disappears--the heat capacity becomes very large and the fluctuations do too. This can be observed as ``critical opalescence'' where the meniscus between the liquid and gas phases disappears and the substance becomes milky and opaque and scatters light. Nice pictures can be found here courtesy of M. de Podesta of UCL, together with further explanation here.