




Previous: Details of the paramagnet calculation
Hyperbolic Trigonometry
Remember that ordinary trig functions are defined as follows:
and it is useful sometimes to use the extra functions
Hyperbolic trig functions are defined similarly:
From the definitions above it is easy to show that
Often we are interested in the small- or large-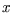 limits of these functions. What we want
is to find a simple function which approximates to a more complicated one in these limits.
So while it is true that as
limits of these functions. What we want
is to find a simple function which approximates to a more complicated one in these limits.
So while it is true that as 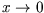 ,
, 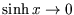 , that is not usually what we want;
what we want is how it tends to zero.
, that is not usually what we want;
what we want is how it tends to zero.
From the small-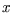 expansion of the exponential
expansion of the exponential
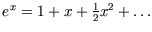 we get
we get
The limit of 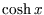 often causes problems; whether we keep the
often causes problems; whether we keep the 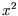 term depends on the context,
given that we want to be able to say more than ``tends to 0'' or ``tends to
term depends on the context,
given that we want to be able to say more than ``tends to 0'' or ``tends to 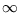 ''. It may be useful
to remember instead
''. It may be useful
to remember instead
The same is true of the exponential:
In a particular problem we find that the energy of a system is
Naively we would say that at high temperatures, as 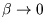 , the denominator vanishes and the energy tends
to infinity. That is
true but not very helpful. If we are more sophisticated we see that the denominator actually tends to
, the denominator vanishes and the energy tends
to infinity. That is
true but not very helpful. If we are more sophisticated we see that the denominator actually tends to
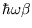 and
and
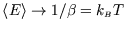 . That is a much more useful prediction, since it can
be verified experimentally.
. That is a much more useful prediction, since it can
be verified experimentally.
The high-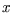 limits are easier;
limits are easier; 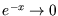 and so
and so





Previous: Details of the paramagnet calculation
Judith McGovern
2004-03-17
![]() limits of these functions. What we want
is to find a simple function which approximates to a more complicated one in these limits.
So while it is true that as
limits of these functions. What we want
is to find a simple function which approximates to a more complicated one in these limits.
So while it is true that as ![]() ,
, ![]() , that is not usually what we want;
what we want is how it tends to zero.
, that is not usually what we want;
what we want is how it tends to zero.
![]() expansion of the exponential
expansion of the exponential
![]() we get
we get
![]() limits are easier;
limits are easier; ![]() and so
and so