Details of the paramagnet calculation

The starting point is the Boltzmann probabilities for the two energy states of a single spin, $\varepsilon_\uparrow=-\mu B$ and $\varepsilon_\downarrow=\mu B$:

$$\begin{eqnarray*} p_\uparrow \!\!\!&=&\!\!\!{e^{ \mu B/ k_{\scriptscriptstyle B... ...+e^{-\mu B/ k_{\scriptscriptstyle B}T}=2{\rm cosh }(\mu B\beta) \end{eqnarray*}$$

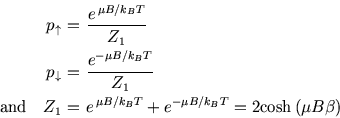
In this simple case both the average energy and magnetisation of a single spin can be found directly from the probabilities:

$$\begin{eqnarray*} \left\langle E_1 \right\rangle \!\!\!&=&\!\!\!\varepsilon_\upa... ...\beta) \qquad\hbox{(using $\beta=1/k_{\scriptscriptstyle B}T$)} \end{eqnarray*}$$

and similarly

$$\begin{eqnarray*} \left\langle m_1 \right\rangle \!\!\!&=&\!\!\!(+\mu) p_\uparrow +(-\mu) p_\downarrow \\ \!\!\!&=&\!\!\!\mu \tanh (\mu B\beta) \end{eqnarray*}$$

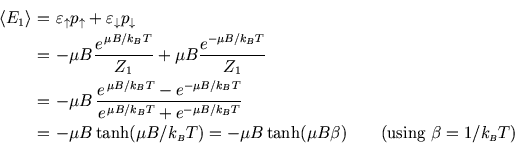
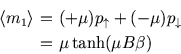
But for things like the entropy which only makes sense for the whole system, and as a warm-up for more complicated cases, we can use the partition function method instead; the results for the energy and magnetisation are the same.

We also have

$$\left\langle F \right\rangle =-k_{\scriptscriptstyle B}T\ln\... ...=-Nk_{\scriptscriptstyle B}T\ln\left(2\cosh(\mu B\beta)\right)$$

and

$$\begin{eqnarray*} \left\langle S \right\rangle \!\!\!&=&\!\!\!-\left({\partial \... ...\cosh(\mu B\beta)\right)-{ \mu B\beta} \tanh(\mu B\beta)\right\} \end{eqnarray*}$$

which does indeed equal $(E-F)/T$.