The speed ![]() of a particle is related to the wavenumber
of a particle is related to the wavenumber ![]() by
by ![]() . We already know the probability
of a particle having
. We already know the probability
of a particle having ![]() in the range
in the range
![]() , and so we can immediately write down the corresponding
probability of the speed being in the range
, and so we can immediately write down the corresponding
probability of the speed being in the range ![]() :
:
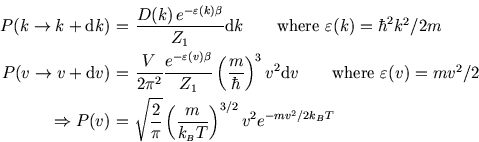
We can find the most probable speed (from
![]() ), as well as the mean speed and the rms speed:
), as well as the mean speed and the rms speed:
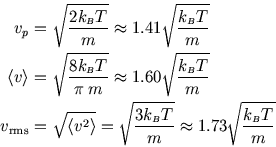
Note that ![]() has disappeared from
has disappeared from ![]() , which can be derived from the Boltzmann distribution in a
purely classical theory provided the normalisation is obtained from requiring the integral of
, which can be derived from the Boltzmann distribution in a
purely classical theory provided the normalisation is obtained from requiring the integral of ![]() to be one.
to be one.
References