| (5.1) |
A kilo of steam starts at a temperature of 250![]() C and 1.4 atmospheres, and
expands and cools to 150
C and 1.4 atmospheres, and
expands and cools to 150![]() C and 1 atmosphere. The surroundings are
at 20
C and 1 atmosphere. The surroundings are
at 20![]() C and 1 atmosphere. What is the maximum amount of useful work that can be
extracted during the expansion? (Treat the steam as an ideal gas, and
take the molar heat capacity
C and 1 atmosphere. What is the maximum amount of useful work that can be
extracted during the expansion? (Treat the steam as an ideal gas, and
take the molar heat capacity
![]() to be 27Jmol
to be 27Jmol![]() K
K![]() .)
.)
for
In both cases
The data comes from the water property calculator at the University of Washington Earth Science website. The first term in
Using the first equation, find the work necessary to perform a reversible isothermal compression
of 1 mole of water from 1 atmosphere to 1000 atmospheres at 25![]() C.
Using the second equation and a Maxwell relation, calculate the decrease in the internal
energy during this process.
C.
Using the second equation and a Maxwell relation, calculate the decrease in the internal
energy during this process.
Hint: the Maxwell relation allows us to find the entropy change ![]() , and as the process
is isothermal we can therefore find
, and as the process
is isothermal we can therefore find ![]() . Watch that final results are in "atm m
. Watch that final results are in "atm m![]() " which needs multiplied
by
" which needs multiplied
by
![]() to convert to Joules.
to convert to Joules.
Compare with qu. (1.iii) where we couldn't find the heat given out
because we didn't have the data above.
- (i)
- Using the fundamental thermodynamic relation and a suitable Maxwell
relation, show that
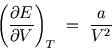
- (ii)
- Hence show that
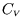 depends only on
depends only on 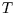 , i.e.
, i.e.
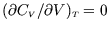
Hint: show first that, since at constant volume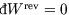 ,
,
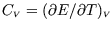 .
.
- (iii)
- By writing
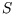 as a function of
as a function of 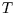 and
and 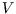 , show that
, show that
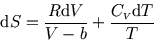
and hence find the analogue of the ideal gas relation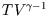 = const. for a reversible adiabatic process involving
a van der Waal gas.
(Take
= const. for a reversible adiabatic process involving
a van der Waal gas.
(Take 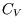 to be constant.)
to be constant.)
See here - (iv)
- Obtain the isobaric coefficient of thermal expansion
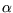
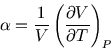
and hence, using expressions from lecture notes, calculate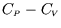 .
.
Hint: for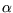 use implicit differentiation rather than solving for
use implicit differentiation rather than solving for 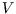 first,
and note that
first,
and note that
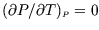 . The answer IS messy! Check your answer for
. The answer IS messy! Check your answer for
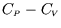 here.
here.