




Previous: 2.13 Heat Capacities
Entropy changes
What is the entropy change during the expansion of a van der Waals gas for which
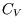 is a constant?
is a constant?
The equation of state for one mole of a van der Waals gas is
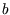 represents the volume taken up by the finite size of the molecules, and
represents the volume taken up by the finite size of the molecules, and 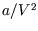 is the reduction
in pressure due to interactions between the molecules. In this way the two most important corrections
neglected in the ideal gas are included. However the heat capacity at constant volume is still independent of
temperature and volume, as in an ideal gas.
is the reduction
in pressure due to interactions between the molecules. In this way the two most important corrections
neglected in the ideal gas are included. However the heat capacity at constant volume is still independent of
temperature and volume, as in an ideal gas.
During an expansion, both the temperature and the volume may change. To calculate the change in entropy,
we need
and
so
Note:
Many problems on this section of the course involve choosing variables, either 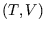 or
or 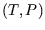 , writing
, writing
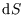 in terms of infinitesimal changes in these variables as in the first line, and then using the definition
of the heat capacities, and a Maxwell relation, to obtain something like the second line.
in terms of infinitesimal changes in these variables as in the first line, and then using the definition
of the heat capacities, and a Maxwell relation, to obtain something like the second line.
Then we can calculate the total entropy change by integrating, first at constant 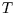 and then at constant
and then at constant 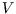 :
:
where in the second integration we used the fact that 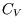 is constant. (We can do this integration because
the two terms in
is constant. (We can do this integration because
the two terms in 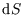 are each functions of one variable only. Given that, the bottom line may be obvious to you
without all the careful intermediate steps.)
are each functions of one variable only. Given that, the bottom line may be obvious to you
without all the careful intermediate steps.)
Note that we have not said what kind of process (reversible or non-reversible, isothermal, adiabatic...) has
taken place; that will go into the relation between 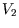 and
and 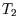 .
.
We can check our result against those we have already calculated for an ideal gas just by setting 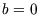 and
using the
correct
and
using the
correct 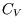 (eg
(eg 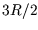 for a monatomic gas), as follows:
First, for an isothermal expansion (
for a monatomic gas), as follows:
First, for an isothermal expansion (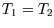 ) we get
) we get
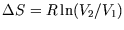 as
before.
as
before.
Also, for a reversible adiabatic expansion we can use
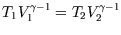 (see here) so
(see here) so
(using 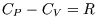 for an ideal gas). But that is as expected: entropy changes for reversible,
adiabatic processes are it always zero! (See here if you have forgotten why...)
for an ideal gas). But that is as expected: entropy changes for reversible,
adiabatic processes are it always zero! (See here if you have forgotten why...)
Conversely, we can use the fact that 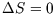 for a reversible adiabatic process to see that for a van der Waals gas,
for a reversible adiabatic process to see that for a van der Waals gas,
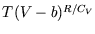 is constant. But
is constant. But 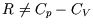 so the exponent isn't
so the exponent isn't 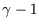 .
.





Previous: 2.13 Heat Capacities
Judith McGovern
2004-03-17
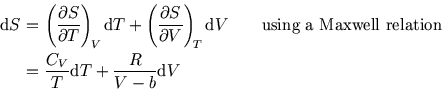
![]() and then at constant
and then at constant ![]() :
:
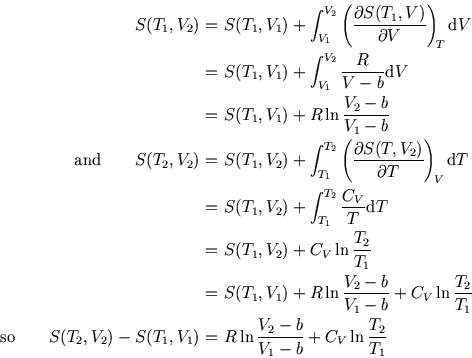
![]() and
and ![]() .
.
![]() and
using the
correct
and
using the
correct ![]() (eg
(eg ![]() for a monatomic gas), as follows:
First, for an isothermal expansion (
for a monatomic gas), as follows:
First, for an isothermal expansion (![]() ) we get
) we get
![]() as
before.
as
before.
![]() (see here) so
(see here) so
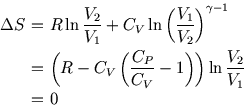
![]() for a reversible adiabatic process to see that for a van der Waals gas,
for a reversible adiabatic process to see that for a van der Waals gas,
![]() is constant. But
is constant. But ![]() so the exponent isn't
so the exponent isn't ![]() .
.