




Next: 2.14 Systems with more than one
Previous: 2.12 Maxwell's Relations
2.13 Heat Capacities
Take-home message: Heat capacities are related to changes of entropy with temperature.
See also subsection on Joule-Thomson expansion here.
A heat capacity 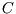 is the temperature change per unit heat absorbed by a system during a reversible process:
is the temperature change per unit heat absorbed by a system during a reversible process:
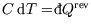 . It is a poor name, since bodies don't contain heat, only energy, but we're stuck
with it. (Note the difference between ``heat capacity (
. It is a poor name, since bodies don't contain heat, only energy, but we're stuck
with it. (Note the difference between ``heat capacity (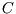 )'' and ``specific heat capacity (
)'' and ``specific heat capacity (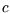 )''; the latter is
the heat capacity per kg or per mole - the units will make clear which.)
)''; the latter is
the heat capacity per kg or per mole - the units will make clear which.)
The heat capacity is is different for different processes. Useful heat capacities are those at constant volume or
constant pressure (for a fluid). Since
we have at constant volume
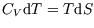 , so
Similarly
, so
Similarly
Furthermore at constant volume, no work is done on the system and so
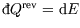 ; hence
; hence
Also (usefully for chemists), at constant pressure
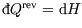 where
where 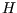 is the
enthalpy, so
is the
enthalpy, so
The specific heat capacity is the heat capacity per unit mass (or per mole). Heat capacities are not
independent of temperature (or pressure) in general, but over a narrow temperature range they are often treated
as such, especially for a solid.
Together with two of Maxwell's relations, we now have expressions for
the partial derivatives of the entropy with respect to all easily manipulable variables (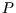 ,
, 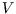 ,
, 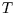 ).
These can be used to derive expressions for the entropy change in real processes. (see here
for an example.)
).
These can be used to derive expressions for the entropy change in real processes. (see here
for an example.)
We can also derive a relation between 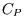 ,
, 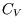 , and other measurable properties of a substance which can be
checked experimentally: if
, and other measurable properties of a substance which can be
checked experimentally: if 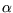 is the isobaric thermal expansivity and
is the isobaric thermal expansivity and 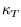 is the isothermal
compressibility
is the isothermal
compressibility
Then we have the relation
which is always greater than zero. (The derivation is set as an exercise.)
This relation is a firm prediction of thermal physics without any approximations whatsoever. It has to be true!
For real gases and compressible liquids and solids it can be checked. For relatively incompressible liquids
and solids it is hard to carry out processes at constant volume so 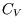 may not be well known and this equation
can be used to predict it.
may not be well known and this equation
can be used to predict it.
For one mole of a van der Waals gas this gives
In the ideal gas limit
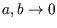 this reduces to
this reduces to 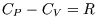 as expected.
as expected.
References
- Mandl 5.3
- Bowley and Sánchez 2.5-6 & E.3
- Adkins 8.1
- Zemansky 10.6, 10.8
Subsections





Next: 2.14 Systems with more than one
Previous: 2.12 Maxwell's Relations
Judith McGovern
2004-03-17
![$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \
$\displaystyle
C_V=T\left({\partial S\over\partial T}\right)_{\!\scriptstyle V}.$ }}$](img329.gif)
![$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \
$\displaystyle
C_P=T\left({\partial S\over\partial T}\right)_{\!\scriptstyle P}.$ }}$](img330.gif)
![]() ; hence
; hence
![]() ,
, ![]() ,
, ![]() ).
These can be used to derive expressions for the entropy change in real processes. (see here
for an example.)
).
These can be used to derive expressions for the entropy change in real processes. (see here
for an example.)
![]() ,
, ![]() , and other measurable properties of a substance which can be
checked experimentally: if
, and other measurable properties of a substance which can be
checked experimentally: if ![]() is the isobaric thermal expansivity and
is the isobaric thermal expansivity and ![]() is the isothermal
compressibility
is the isothermal
compressibility