2.14 Systems with more than one component

Take-home message: The chemical potential is important wherever the number of molecules in a system isn't fixed.

If we have a mixture of two substances present, the internal energy and all the other thermodynamical potentials will depend on how much of each is present, since there will be interactions between the molecules of each.

Here we focus on the Gibbs free energy, since the relevant conditions are usually those of fixed temperature and pressure.

We have $G=G(T,P,N_1,N_2)$ where $N_1$ and $N_2$ are the number of molecules of each substance. (This is easily generalised more than two components.) So

$${\rm d}G= \left({\partial G\over\partial T}\right)_{\!\scrip... ...G\over\partial N_2}\right)_{\!\scriptstyle T,P,N_1} {\rm d}N_2$$

Now the first two partial derivatives are $-S$ and $V$ as before. We define

$$\mu_1=\left({\partial G\over\partial N_1}\right)_{\!\scripts... ...{\partial G\over\partial N_2}\right)_{\!\scriptstyle T,P,N_1}$$

giving

$${\rm d}G=-S{\rm d}T+V{\rm d}P+\mu_1{\rm d}N_1+\mu_2{\rm d}N_2$$

$\mu_1$ is called the chemical potential of substance 1. But what is its significance?

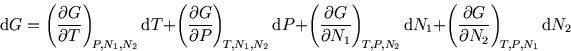
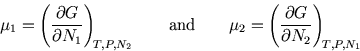
First, imagine only one substance present. Then

$$\mu=\left({\partial G\over\partial N}\right)_{\!\scriptstyle T,P}$$

But $G$ is extensive, and $P$ and $T$ are intensive, so $G$ must be directly proportional to $N$: $G(T,P,N)=N g(T,P)$ (where $g$ is the Gibbs free energy per molecule), and so $\mu=g$.

So for a single component system, $\mu$ is just the Gibbs free energy per molecule.

But for a two component system, $G$ depends not only on the extensive variable $N_1+N_2$ but also on the ratio $N_1/N_2$, which is intensive. The Gibbs free energy per molecule of one substance can depend on the concentration of the other. All we can say is $\mu_1$ is the extra Gibbs free energy per added molecule of substance 1. If substance 1 is ethanol and substance 2 water, the chemical potential of ethanol is different in beer (5%) and vodka (40%).

However for ideal gases, since there are no intermolecular interactions, the Gibbs free energies are independent and additive: $G=\mu_1N_1+\mu_2N_2$.

From $E=G-PV+TS$, $F=G-PV$ and $H=G+TS$ (see here), we see that the term $\mu_1{\rm d}N_1+\mu_2{\rm d}N_2$ is added to ${\rm d}E$, ${\rm d}F$ and ${\rm d}H$ also, and

$$\mu_1=\left({\partial E\over\partial N_1}\right)_{\!\scripts... ...{\partial H\over\partial N_1}\right)_{\!\scriptstyle S,P,N_2}.$$

An important use of chemical potentials is in chemical reactions. But it is important to physicists too. Not all reactions are chemical: in a neutron star, neutrons, protons and electrons can interact via ${\rm p}+{\rm e^-}\rightleftharpoons{\rm n}$; they reach an equilibrium at which the chemical potentials on either side of the reaction are equal. This is heavily biased toward neutrons, because the chemical potential of the light electron is much higher for a given concentration than that of the heavy proton or neutron. (Why? I'm afraid that must wait till next year!)

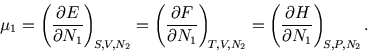
The chemical potential also governs systems which can exchange particles with a reservoir, and that is the context in which we will meet it in statistical physics.

Note: the use of $\mu$ to mean magnetic moment as well as chemical potential should never confuse, as magnets tend to have fixed numbers of atoms.

If like most students you find the chemical potential mystifying, look at this helpful slide from Peter Saeta of Harvey Mudd College. The last point will only become clear once we've done Gibbs distributions at the end of the course.

References

• Mandl 8.1
• Bowley and Sánchez 2.9
• Adkins 11.3
• Zemansky 11.6