2.8 Thermodynamic potentials

Take-home message: Other quantities can be defined which, under common experimental conditions, are more relevant than the energy.

Let's look again at the fundamental thermodynamic relation for a hydrodynamic system: ${\rm d}E=T{\rm d}S-P{\rm d}V$.

This suggests that the natural variable in which to express $E$ are $S$ and $V$: $E=E(S,V)$. That means that energy will be unchanged for processes at constant volume and entropy--not the most common experimental conditions. It is useful to introduce other functions of state, called ``thermodynamic potentials'', which are conserved, or whose change is easily calculated, in common experimental conditions.

These are

• Enthalpy:
  $\mbox{\colorbox{yellow}{ \parbox{10cm}{ \begin{eqnarray*} H=E+PV \qquad\hbox{so... ...V\nonumber \\ \!\!\!&=&\!\!\!T{\rm d}S+V{\rm d}P \nonumber \end{eqnarray*} }}}$
  At constant pressure (such as chemical reactions in a test tube), ${\rm d}P=0$ and so ${\rm d}H={}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}Q^{\rm rev}$. Heats of reaction are usually measured as enthalpies of reaction.

• Helmholtz free Energy:
  $\mbox{\colorbox{yellow}{ \parbox{10cm}{\begin{eqnarray*} F=E-TS \qquad\hbox{so}... ...\nonumber \\ \!\!\!&=&\!\!\!-S{\rm d}T- P{\rm d}V \nonumber \end{eqnarray*}}}}$
  The Helmholtz free energy is constant at constant temperature and volume. It plays a key role in statistical physics.

• Gibbs Free Energy:
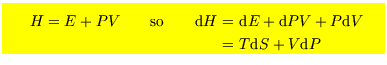
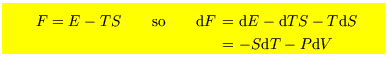
  $\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle G=E-TS+PV \qquad\hbox{so}\qquad {\rm d}G=-S{\rm d}T+V{\rm d}P $ }}$

  The Gibbs free energy is constant if the temperature and pressure are constant. These are the conditions under which phase transitions (melting, boiling) take place, and are also relevant to chemical equilibrium.

Note that Enthalpy and Gibbs free energy are only relevant to hydrodynamic systems for which ${}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}W^{\rm rev}=-P{\rm d}V$. However the energy and the Helmholtz free energy is more general, with ${\rm d}E= T{\rm d}S+ {}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}W^{\rm rev}$ and ${\rm d}F=-S{\rm d}T+ {}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}W^{\rm rev}$

References

• Mandl 4.4-5
• Bowley and Sánchez 2.6
• Adkins 7.1
• Zemansky 10.1-3 (Warning: Zemansky uses $A$ for the Helmholtz free energy!)