2.15 Chemical reactions

Take-home message: At equilibrium the chemical potential of reactants and products are equal.

The treatment of chemical reactions is very like that of phase transitions. Again, we are considering conditions of constant temperature and pressure, and the question is the following: how far will a reaction go?

First consider the simplest case of a reaction with only one reactant and one product: ${\rm A}\rightleftharpoons{\rm B}$. An example is the interconversion of n-pentane and isopentane (or pentane and methyl-butane, for those of us who learned our chemistry in the last thirty years).

Spontaneous changes will minimise the Gibbs free energy (see here). With temperature and pressure fixed only the numbers of A and B can change. Since they can only interconvert, ${\rm d}N_A=-{\rm d}N_B$ and

$${\rm d}G = \mu_A {\rm d}N_A+\mu_B {\rm d}N_B=(\mu_A-\mu_B){\rm d}N_A$$

So if $\mu_A>\mu_B$, A will convert to B, but if $\mu_B>\mu_A$, the opposite will happen. So at equilibrium, when no further changes happen, the chemical potentials must be equal. (Remember that the chemical potentials are functions of concentration, so they will change as the reaction proceed.)

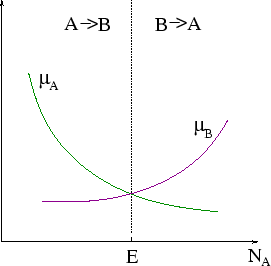
In the figure ``E'' marks the equilibrium concentration, at the point where $\mu_A=\mu_B$.

If there are more reactants or products, say $\rm A+B\rightleftharpoons C+D$, the numbers of A, B, C and D change together: ${\rm d}N_A={\rm d}N_B=-{\rm d}N_C=-{\rm d}N_D$. So

$${\rm d}G=\mu_A {\rm d}N_A+\mu_B{\rm d}N_B+\mu_C{\rm d}N_C+\mu_D{\rm d}N_D=(\mu_A +\mu_B-\mu_C-\mu_D){\rm d}N_A$$

and equilibrium is when $\mu_A +\mu_B=\mu_C+\mu_D$.

This result is general: equilibrium is reached when the sum of the chemical potential of the reactants equals that of the products. For reactants and products that can be treated as ideal gases, we can go further and make predictions about relative concentrations at equilibrium, see here.

References

• Mandl 11.9
• Bowley and Sánchez 9.2
• Adkins 11.4