2.10 Use of Gibbs Free Energy: Phase Transitions

Take-home message: The Gibbs free energies of two coexisting phases is the same.

We are interested in the cases where two phases of the same substance can coexist. An example is ice in water at $0^{\rm o}$C: if no heat is exchanged with the surroundings, the mixture will persist indefinitely.

In practical cases we are interested in charting the behaviour of the substance as a function of external temperature and pressure. For most choices, only one phase will persist at equilibrium - water, or ice, or vapour, for example. But for certain choices, two or even three phases may coexist.

The phase diagram for water is shown below. (Image ©M. Blaber, Florida State University)

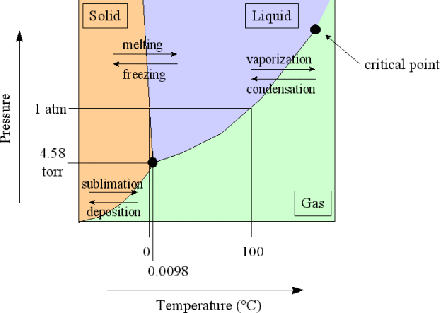
It differs from a generic substance in the backward slope of the ice-water coexistence line: putting ice under pressure may cause it to melt, whereas most liquids close to their freezing point will freeze under pressure.

What determines the lines of phase coexistence?

Consider a system of two phases, 1 (say gas) and 2 (say liquid) at a fixed pressure and temperature.

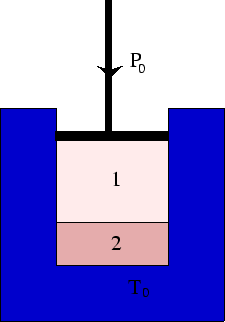
From the fact that the system will minimise its Gibbs free energy, we can derive the following condition for phase coexistence: The Gibbs free energy per unit mass in each phase is the same.

At temperatures and pressures not on the coexistence line the Gibbs free energy of one phase will be lower than the other, and only the phase with the lower energy will be present at equilibrium.

Suppose we know the location of one point on a coexistence line (for instance the melting point at atmospheric pressure). Can we discover other points - for instance, the melting point at a higher or lower pressure? The answer is yes, for very small changes: in fact we can discover the slope of the line:

$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle {{\rm d}P\over{\rm d}T}={L\over T \Delta V} $ }}$

where $L$ is the latent heat of the transition for some quantity of the substance, and $\Delta V$ is the volume change of the same quantity as it undergoes the transition. This is called the Clausius-Clapeyron equation. (Details of the derivation here.)

We can use this equation to estimate the boiling point of water at the top of Mount Everest, where the pressure is only about a third of that at sea-level, to be $82^{\rm o}$C.

(Input data: pressure at the top of Everest is 0.36 atmospheres, the density of water vapour at $100^{\rm o}$C is 0.598 kg/m$^3$ and the latent heat is $2.257\times 10^3$ J/g.)

Of course this estimate requires assuming that the phase coexistence line has negligible curvature over a fairly large range, so it is no surprise that the result is only approximate. By looking at the phase diagram above you should be able to say if the true temperature is higher or lower.

References

• Mandl 8.1-4
• Bowley and Sánchez 11.1, 11.4-5 (note they refer to the ``Clapeyron Equation'')
• Adkins 10.3-5
• Zemansky 11.3-4