The Clausius-Clapeyron Equation

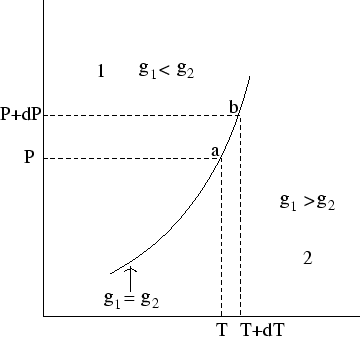
Suppose we know the location of one point on a coexistence line (for instance the melting point at atmospheric pressure). Can we discover other points - for instance, the melting point at a higher or lower pressure? The answer is yes, for very small changes: in fact we can discover the slope of the line.

At both $a$ and $b$ the two phases are in equilibrium, so the specific Gibbs free energies of the two phases at each point are the same: $g_1^{(a)}=g_2^{(a)}$ and $g_1^{(b)}=g_2^{(b)}$. So if ${\rm d}g$ is the difference in the Gibbs free energy between the two points, it is the same for both phases: ${\rm d}g_1={\rm d}g_2$. But (using small letters $s$ and $v$ to denote specific entropy and volume),

$$\begin{eqnarray*} {\rm d}g_1\!\!\!&=&\!\!\!-s_1 {\rm d}T+v_1 {\rm d}P \nonum... ... d}P\over{\rm d}T}\!\!\!&=&\!\!\!{S_2-S_1\over V_2-V_1}\nonumber \end{eqnarray*}$$

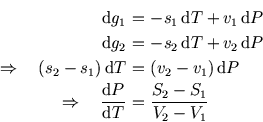
The is called the Clausius-Clapeyron equation, and it relates the slope along the coexistence line with the change in entropy and volume of the substance as it crosses the line, ie changes phase.

This doesn't look very useful, as we can't measure entropy directly. However, using $\Delta S=Q/T$ for an isothermal process, we can find the change in entropy at a phase transition from the latent heat $L$, and so the more useful form of the equation is

$${{\rm d}P\over{\rm d}T}={L\over T \Delta V}.$$