Boiling point on Everest

We take the pressure at the top of Everest to be 0.36 atmospheres, the density of water vapour at $100^{\rm o}$C to be 0.598 kg/m$^3$ and the latent heat to be $2.257\times 10^3$ J/g.

The change in volume of 1 gram is well approximated by just the volume of the gas phase, since the vapour is about a thousand times less dense than the liquid: $\Delta V=V_g-V_l\approx V_g=1/\rho_g$.

So

$$\begin{eqnarray*} {{\rm d}P\over{\rm d}T}\!\!\!&=&\!\!\!{L\over T \Delta V}={L \... ...elta P /(3.6\times10^3 \hbox{Pa/K})=-18^{\rm o}{\rm C}\nonumber \end{eqnarray*}$$

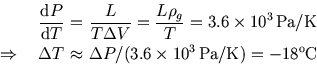
Did you get the right numbers? If not, did you remember to convert the latent heat and the density to refer to the same amount of water (1 kg or 1 g).