2.11 Available work

Take-home message: The availability is a measure of the useful work which can be extracted from a system.

Here we consider the amount of useful work which can be extracted from a system which is initially out of equilibrium with its surroundings, which are at temperature $T_0$ and pressure $P_0$.

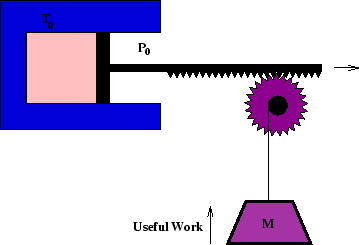
There are two factor which limit this. One is that if the system expands, it has to overcome atmospheric pressure before doing any useful work, so $P_0\Delta V$ is wasted. The other is that if its entropy decreases (as in cooling) the entropy of the surrounding must increase enough to compensate. The system must discard heat $Q$ to the surroundings so that $\Delta S+Q/T_0\ge0$.

So of the total energy decrease of the system, $\Delta E$, the amount available to do work is

$$W^{\rm useful}=(-\Delta E)-Q-P_0\Delta V\le-\Delta E+T_0\Delta S-P_0\Delta V=-\Delta A$$

where the availability $A$ is $E-T_0 S-P_0 V$.

The equality is satisfied for reversible processes, which maximises the useful work available. (To cool reversibly with only a single cold reservoir would require the use of a heat engine to extract the heat, rather than the direct transfer depicted above.)

This explains why the availability, which we have met in a slightly different context, is so called.

Remember that it is the temperature and pressure of the surroundings that enter, not that of the system (though they end up the same).

Follow this link for an example.

References

• Mandl 4.6
• Adkins 10.2