PC2352 Examples 2

The web version of this sheet contains links and hints in this font.

2.

Calculate the work done on the system in the following reversible processes:

(i) Isothermal compression of 1 mole of an ideal gas at 273K from 1 to 2atm pressure. (1atm=1.013$\times 10^5$Pa.)
See here for a similar example.

(ii) Adiabatic compression of 1 mole of an ideal gas initially at 273K from 1 to 2atm pressure. (Take $\gamma = C_{P}/C_{V} = 1.4$ ).
Adiabatic compression is covered in this example.

(iii) Isothermal compression of 1 mole of water at 273K from 1 to 2atm pressure. The density of water is 1000kgm$^{-3}$. The bulk modulus $B$ of water (at 273K and in the pressure range indicated) is $2 \times 10^{9}$Nm$^{-2}$. The bulk modulus is the elastic modulus that relates the volume change $\Delta V$ to the pressure change $\Delta P$ that produces it by $\Delta P = -B \Delta V/V_{0}$, where $V_{0}$ is the initial volume.
Remember, water is not an ideal gas! We can't use PV=nRT! Instead use the information in the question to write the ${\rm d}V$ of $-P{\rm d}V$ in terms of ${\rm d}P$.

(iv) Isothermal magnetization of 1 mole of a paramagnetic sample at 273K from an external field of 1T to an external field of 2T. Assume that the equation of state is

$$M = \frac {CB}{\mu_{0}T}$$

with $C = 0.1$K and that the molar volume is $30 \times 10^{-6}$m$^{3}$. (Use ${}\raise0.44ex\hbox{\bf\symbol{'040}}\llap{d}W = -VM{\rm d}B$ as introduced here).
A model paramagnet is described here; we will meet it again later in the course.

(v) Isothermal stretching of an elastic string from 0.1m to 0.2m at 273K. The equation of state linking the tension $\Gamma$ to the length $l$ of the string is

$$\Gamma = KT \left[ \frac{l}{l_{1}} - \frac{l_{1}^{2}}{l^{2}} \right]$$

where $K = 0.1$NK$^{-1}$ and $l_{1} = 0.1$m is the unstretched length.
The work done in stretching a string is given here - but try to guess it first.

In cases (i), (ii) and (iv), how much heat is absorbed or given out by the system? You may assume that the internal energy of the paramagnet is $E=-VMB$.
Here we use the first law, so we can only find the answer for those cases where we know the internal energy - as we do for an ideal gas and an ideal paramagnet.

3.

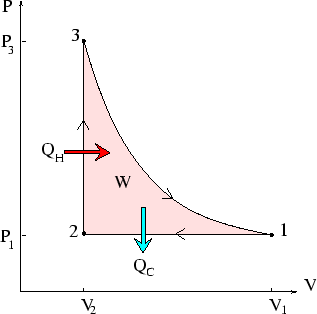
A quantity of ideal gas is taken through the reversible cycle depicted above, where the three processes are isobaric, isochoric and adiabatic respectively. Calculate the work done on the system, and the heat absorbed, during each stage, and check that the total work done by the system is equal to the net heat absorbed--which equals $C_{\scriptscriptstyle V}(T_3-T_2)-C_{\scriptscriptstyle P}(T_1-T_2)$.

Hence show that the efficiency of the system as a heat engine is

$$\begin{eqnarray*} \eta\!\!\!&=&\!\!\!1-\gamma\left({T_1-T_2 \over T_3-T_2}\right... ...-{\gamma\over r}\left({1-r\over 1-r^\gamma}\right){T_2\over T_3} \end{eqnarray*}$$

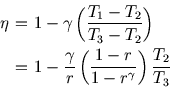
where $r=V_2/V_1$.

The Otto cycle is covered here. Only the isobaric stroke is new.

This is lower than that of a Carnot engine operating between the lowest and highest temperatures attained in the cycle ($T_2$ and $T_3$ respectively). This is hard to prove algebraically, but using your graphical calculator you should be able to convince yourself that the function of $r$ multiplying $T_2/ T_3$ is greater than 1 for all positive $r$ less than 1 (with $\gamma>1$).
It's much easier to prove for the Otto cycle. Try it!