PC1672 Advanced dynamics

4.4 Moment-of-inertia tensor

The moment-of-inertia tensor relates the angular momentum of a rigid body to its angular velocity,

$\begin{displaymath}{\bf L}=\underline{\underline{\bf I}}\cdot\hbox{\boldmath {$\omega$}}\end{displaymath}$

The corresponding rotational kinetic energy has the form

$\begin{displaymath}T={1\over 2}\hbox{\boldmath {$\omega$}}\cdot \underline{\underline{\bf I}}\cdot\hbox{\boldmath {$\omega$}}\end{displaymath}$

The tensor can be written

$\begin{displaymath}\underline{\underline{\bf I}}=\sum_\alpha m_\alpha\left[({\bf... ...e{\underline{\bf 1}}-{\bf x}_\alpha\otimes{\bf x}_\alpha\right]\end{displaymath}$

Its components are

$\begin{displaymath}I_{ij}=\sum_\alpha m_\alpha\left[({\bf x}_\alpha^2)\delta_{ij} -x_{\alpha i}x_{\alpha j}\right]\end{displaymath}$

The moment-of-inertia is symmetric

$\begin{displaymath}\underline{\underline{\bf I}}^{\rm T}=\underline{\underline{\bf I}}\end{displaymath}$

In other words, its components form a real symmetric $3\times 3$ matrix,

$\begin{displaymath}I_{ij}=I_{ji}\end{displaymath}$

This means that the tensor has only six independent components. These include the three diagonal ones, for example $I_{11}$ which has the form

$\begin{displaymath}I_{11}=\sum_\alpha m_\alpha \left(x_{\alpha 2}^2+x_{\alpha 3}^2\right)\end{displaymath}$

We recognise this as the ordinary moment of inertia about the

-axis (involving the square of the distance of each atom from the axis). There are also three independent off-diagonal components, for example $I_{12}$ which has the form

$\begin{displaymath}I_{12}=-\sum_\alpha m_\alpha x_{\alpha 1} x_{\alpha 2}\end{displaymath}$

and is known as a product of inertia.

If we treat the body as a continuous distribution of matter with density $\rho({\bf x})$ then we can replace the sum over atoms by an integral over volume:

$\begin{displaymath}I_{ij}=\int\!\!\int\limits_V\!\!\int\rho({\bf x})\left[{\bf x}^2\delta_{ij} -x_i x_j\right]{\rm d}V\end{displaymath}$

The components of $\underline{\underline{\bf I}}$ can then be evaluated by using the usual techniques for multiple integration.

For a thin flat plate the inertia tensor has a particularly simple form. If the plate lies in the plane we have

$\begin{displaymath}I_{13}=I_{23}=0\end{displaymath}$

In addition, the moment of inertia about the

-axis, normal to the plate, is given by the perpendicular axes theorem:

$\begin{displaymath}I_{33}=I_{11}+I_{22}\end{displaymath}$

Hence we need to calculate only $I_{11}$ , $I_{22}$ and $I_{12}$ for such a body. For example $I_{11}$ can be written

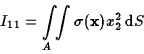
$\begin{displaymath}I_{11}=\int\limits_A\!\!\int\sigma({\bf x})x_2^2\,{\rm d}S\end{displaymath}$

where $\sigma({\bf x})$ is the surface mass density of the plate.

Textbook references

K&K 7.6
F&C 9.1
B&O 6.7
M 12.1
M&T 11.1

Mike Birse
17th May 2000