PC1672 Advanced dynamics

4.5 Principal axes

A rigid body is dynamically balanced when its angular momentum is parallel to its angular velocity:

$\begin{displaymath}{\bf L}=\underline{\underline{\bf I}}\cdot\hbox{\boldmath {$\omega$}} =I\hbox{\boldmath {$\omega$}}\end{displaymath}$

where

is some (scalar) number. For this to be true, the angular velocity $\hbox{\boldmath {$\omega$ }}$ must point along a principal axis of the moment-of-inertia tensor. The corresponding value of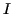

is called a principal moment of inertia.

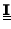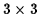The principal axes are the eigenvectors of the tensor $\underline{\underline{\bf I}}$ and the principal moments are its eigenvalues. In component form, we can find these by solving a $3\times 3$ eigenvalue problem. The eigenvectors satisfy the set of linear equations

$\begin{displaymath}\pmatrix{I_{11}-\lambda&I_{12}&I_{13}\cr I_{21}&I_{22}-\lambd... ...32}&I_{33}-\lambda}\pmatrix{\omega_1\cr \omega_2\cr \omega_3}=0\end{displaymath}$

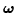Nontrivial solutions for $\hbox{\boldmath {$\omega$ }}$ exist only if the determinant vanishes,

$\begin{displaymath}\left\vert\matrix{I_{11}-\lambda&I_{12}&I_{13}\cr I_{21}&I_{22}-\lambda&I_{23}\cr I_{31}&I_{32}&I_{33}-\lambda}\right\vert=0\end{displaymath}$

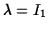This characteristic equation is a cubic in $\lambda$ , with three solutions: $\lambda=I_1$ ,

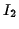and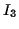

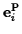. To find the eigenvectors, we substitute in turn each eigenvalue back into the set of linear equations. Only two of the equations will be independent and we can use these to determine the direction of the corresponding eigenvector. The magnitudes of the eigenvectors are not determined and so we often choose unit eigenvectors ${\bf e}_i^{\rm P}$ to specify the directions of the principal axes.

The moment-of-inertia tensor is symmetric and so its eigenvalues and eigenvectors have similar properties to those of a real symmetric matrix:

The principal moments (eigenvalues) are real:

$\begin{displaymath}I_i=I_i^*\end{displaymath}$
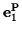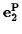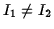If ${\bf e}_1^{\rm P}$ and ${\bf e}_2^{\rm P}$ are principal axes (eigenvectors) corresponding to different principal moments, $I_1\neq I_2$ , then these axes are orthogonal:

$\begin{displaymath}{\bf e}_1^{\rm P}\cdot{\bf e}_2^{\rm P}=0\end{displaymath}$

In some cases a rigid body has degenerate principal moments,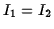

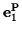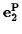(when the characteristic equation has a repeated root). Then any vector in the plane of ${\bf e}_1^{\rm P}$ and ${\bf e}_2^{\rm P}$ is also a principal axis and we can choose any convenient pair of vectors in this plane as principal axes. To summarise:

Any rigid body has three principal axes, which are mutually orthogonal, or can be chosen to be so.

If a body has an axis of symmetry then rotations about that axis will be dynamically balanced; in other words that axis is a principal axis. Hence we can use the symmetries of a body to recognise principal axes:

Any axis of symmetry through the origin O is a principal axis for rotations about O.
The normal to a plane of reflection symmetry through O is a principal axis. (The normal to a flat plate is a particularly important example of this.)

By using these along with the orthogonality property above, we can determine all three principal axes for many bodies with simple shapes. If we choose our coordinate axes to lie along these directions, then we can find the principal moments without having to solve the corresponding eigenvalue problem: they are just the moments of inertia about our three principal axes.

Textbook references

K&K (7.6)
F&C 9.2
B&O 7.6
M 12.4 (12.6)
M&T 11.4
B 10.4, 10.5 for eigenvalues and eigenvectors of matrices

Mike Birse
17th May 2000