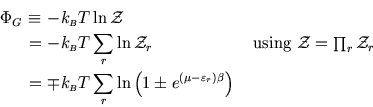
The last time we calculated the properties of an ideal gas, we regarded the particle number as fixed, but the energy as variable (the temperature being fixed.) However we knew that for a large system, fluctuations are small, and the results will be essentially the same as the more difficult problem of an isolated gas with fixed energy.
This raises the question of whether we couldn't obtain the same results regarding the particle number as variable also, fixing instead the chemical potential. The answer is that we can of course, as the following shows.
From the previous sections on the Gibbs distribution and the ideal gas of bosons or fermions, we have
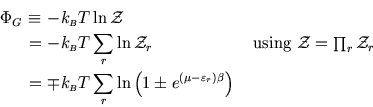
Now imagine that
![]() , which requires
, which requires ![]() to be large and negative. Never mind for a moment
what that means physically. Then, using
to be large and negative. Never mind for a moment
what that means physically. Then, using
![]() for small
for small ![]() , we get
, we get
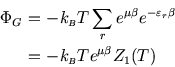
From ![]() we can find the average particle number:
we can find the average particle number:
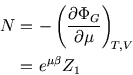
Finally, since
![]() , we have
, we have
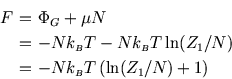
However this is exactly what we get from
![]() with
with
![]() . Thus we recover all our
previous results.
. Thus we recover all our
previous results.
References