5.6 Electrons in a metal

Take-home message: The properties of Fermi gases such as electrons in metals and neutron stars are dramatically different from ideal classical gases.

We have already seen that for electrons in metal, the number of states with energies of order $k_{\scriptscriptstyle B}T$ is much less that the number of electrons to be accommodated. Because electrons are fermions, they can't occupy the same levels, so levels up to an energy far above $k_{\scriptscriptstyle B}T$ will need to be filled. The occupancy is given by $N(\varepsilon)=1/( e^{(\varepsilon-\mu)\beta}+1)$ which is plotted below:

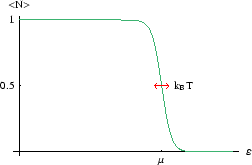
Only levels within a few $k_{\scriptscriptstyle B}T$ of $\mu$ have occupancies which are different from 0 or 1. But what is $\mu$? Normal metals exist in isolated chunks, and are not in contact with ``electron reservoirs''. The answer is that we choose it so that the metal contains the right number of electrons: $\left\langle N \right\rangle =\int_0^\infty\!D(k)N(k){\rm d}k\equiv N$. For copper at room temperature, $\mu\approx 7$ eV, whereas $k_{\scriptscriptstyle B}T\approx 1/40$ eV

The fact that thermal fluctuations affect only a small fraction of all the electrons has a number of consequences. for instance the electronic heat capacity is much less than the $\frac 3 2 k_{\scriptscriptstyle B}T$ predicted by equipartition. Most of the resistance to compression of metals is due to the fact that, if the volume is reduced, the energy of all the single-electron states increases, increasing the electronic internal energy.

References

• Mandl
• Bowley and Sánchez 10.4.2