There are interesting properties of gases of bosonic atoms, but they are beyond the scope of this course. However
black-body of cavity radiation can be considered as a gas of photons. The walls of the cavity act as a heat bath;
however as photons don't exist in the walls (only energy does) the chemical potential is zero:
![]() .
The density of states for the photon gas
is just twice the usual density of states (to allow for the two polarisation states) and the energy of a photon with
wavenumber
.
The density of states for the photon gas
is just twice the usual density of states (to allow for the two polarisation states) and the energy of a photon with
wavenumber ![]() is
is
![]() . The total energy in the cavity is
. The total energy in the cavity is
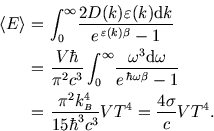
(The factor of ![]() comes from the connection between the cavity energy and the emissivity of a perfect black body,
which is given by the formula for effusion from a small hole
comes from the connection between the cavity energy and the emissivity of a perfect black body,
which is given by the formula for effusion from a small hole
![]() .)
.)
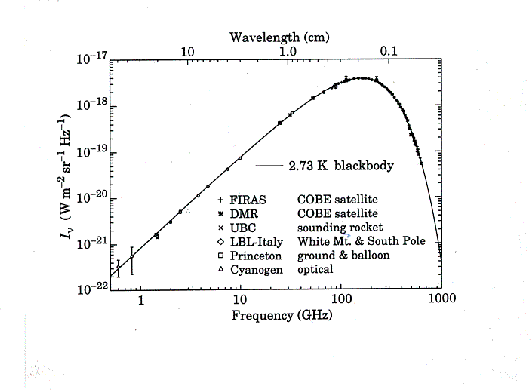
Below is a plot of the cosmic microwave background at a range of frequencies, obtained from a variety of experiments,
compared with the Planck distribution for ![]() K (©Douglas Scott of the University of British Columbia).
The agreement is excellent.
K (©Douglas Scott of the University of British Columbia).
The agreement is excellent.
References