

Next: Hint 9
Up: Examples 4
Previous: Hint 7
Hint 8
Taking 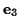 to be the principal axis normal to the disc,
the principal moments can be expressed (using the perpendicular axes theorem)
as
to be the principal axis normal to the disc,
the principal moments can be expressed (using the perpendicular axes theorem)
as
In this case Euler's equations simplify to
These equations are very similar to the ones for the freely rotating symmetric
top. They can be solved using the same trick as in the case of free rotation.
The complex ``coordinate" 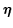 defined as in the previous hint satisfies the
first-order differential equation
defined as in the previous hint satisfies the
first-order differential equation
This has solutions of the form
Mike Birse
2000-03-31
![]() to be the principal axis normal to the disc,
the principal moments can be expressed (using the perpendicular axes theorem)
as
to be the principal axis normal to the disc,
the principal moments can be expressed (using the perpendicular axes theorem)
as