

Next: About this document ...
Up: Examples 4
Previous: Hint 8
Hint 9
The rate of precession of a symmetric top rotating about an axis
close to the vertical has one of two possible values
where 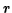 is the distance of its centre of mass from the point of support.
This motion is stable only if
is the distance of its centre of mass from the point of support.
This motion is stable only if 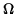 is real. This holds for
is real. This holds for
For the pencil, the minimum 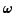 for stability is about 2900 rad s
for stability is about 2900 rad s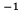 !
!
Mike Birse
2000-03-31