

Next: Hint 8
Up: Examples 4
Previous: Hint 6
Hint 7
The principal axes are 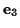 ,
normal to the plate, and any
pair of perpendicular axes lying in the plane of the plate. The principal
moment about the
,
normal to the plate, and any
pair of perpendicular axes lying in the plane of the plate. The principal
moment about the 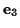 axis is
axis is
and, by the perpendicular axes theorem, the principal moments about the
other two axes are
(a) Since 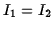 ,
the Euler's equation for
,
the Euler's equation for 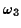 becomes
becomes
Hence 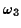 must be a constant.
must be a constant.
(b) The other two equations simplify to
Note that these equations are a special case of the ones for the freely
rotating symmetric top. They can be solved by differentiating one equation with
respect to 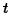 and using the other to get a second-order differential equation
for either
and using the other to get a second-order differential equation
for either 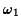 or
or 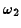 .
Alternatively we can define a complex
``coordinate"
.
Alternatively we can define a complex
``coordinate"
This satisfies the first-order differential equation
which has solutions of the form
where 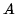 ,
,
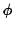 and
and 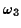 are constants. Interpret this result in terms
of the precession of
are constants. Interpret this result in terms
of the precession of
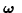 .
.


Next: Hint 8
Up: Examples 4
Previous: Hint 6
Mike Birse
2000-03-31
![]() ,
normal to the plate, and any
pair of perpendicular axes lying in the plane of the plate. The principal
moment about the
,
normal to the plate, and any
pair of perpendicular axes lying in the plane of the plate. The principal
moment about the ![]() axis is
axis is
![]() ,
the Euler's equation for
,
the Euler's equation for ![]() becomes
becomes