

Next: Hint 4
Up: 1999 exam paper
Previous: Hint 2
Hint 3
The station has an axis of symmetry and so 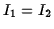 .
For a constant torque
about the (body-fixed)
.
For a constant torque
about the (body-fixed) 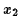 -axis, Euler's equations are
-axis, Euler's equations are
The third equation implies that
The first two equations can be written
where
These can be solved either by differentiating the second with respect to 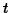 and using the first to eliminate
and using the first to eliminate
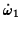 or by introducing the complex
variable
or by introducing the complex
variable
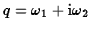 .
The general solution is
.
The general solution is
Imposing the initial condition that
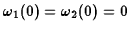 fixes the
constant
fixes the
constant
Taking real and imaginary parts of 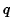 gives the forms for
gives the forms for
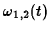 in the question.
in the question.
At
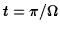 the angular velocity is
the angular velocity is
Since our axes lie along the principal axes, the angular momentum is just


Next: Hint 4
Up: 1999 exam paper
Previous: Hint 2
Mike Birse
2000-03-31
![]() .
For a constant torque
about the (body-fixed)
.
For a constant torque
about the (body-fixed) ![]() -axis, Euler's equations are
-axis, Euler's equations are
![]() the angular velocity is
the angular velocity is