

Next: About this document ...
Up: 1999 exam paper
Previous: Hint 3
Hint 4
(a) In terms of the preigee distance 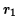 and the apogee distance
and the apogee distance 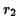 ,
the
semimajor axis is
,
the
semimajor axis is
The eccentricity is
(b) The energy in orbit is
(which the same as for a circular orbit of radius 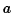 ).
The energy at rest on the Earth's surface is purely potential,
).
The energy at rest on the Earth's surface is purely potential,
Hence an energy
is needed.
(c) At perigee the energy consists of kinetic and potential pieces,
Using the expression for the total energy above gives
(d) At perigee the velocity is perpendicular to the radius and so the
angular momentum is
(and points along the normal to the plane of the orbit).
Mike Birse
2000-03-31
![]() and the apogee distance
and the apogee distance ![]() ,
the
semimajor axis is
,
the
semimajor axis is