




Previous: 2.12 Maxwell's Relations
The rules of partial differentiation
 Identify the independent variables, eg
Identify the independent variables, eg 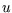 and
and 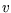 .
.
 If
If 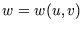 , the partial derivative of
, the partial derivative of 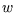 with respect to
with respect to 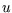 is obtained by holding
is obtained by holding 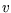 constant;
it is written
constant;
it is written
 It follows that
It follows that
 The order of differentiation doesn't matter:
The order of differentiation doesn't matter:
 The change in
The change in 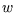 as a result of changes in
as a result of changes in 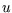 and
and 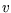 is
is
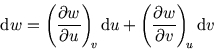 |
(2.1) |
 We could take
We could take 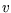 and
and 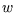 to be the independent variables, with
to be the independent variables, with 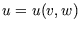 .
Now the partial derivatives are
.
Now the partial derivatives are
Note the first is no longer required to be zero - it's 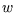 , not
, not 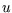 , that is held constant. In this case,
, that is held constant. In this case,
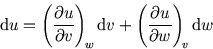 |
(2.2) |
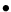 By comparing (2.1) and (2.2) with
By comparing (2.1) and (2.2) with 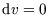 , we see that
, we see that
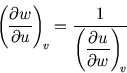 |
(2.3) |
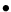 From (2.1) we have
From (2.1) we have
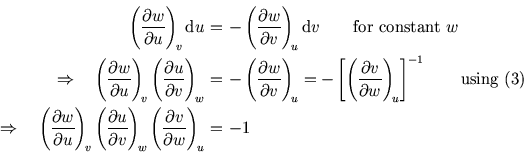 |
(2.4) |
In the second line, ``dividing 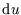 by
by 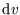 '' gave
'' gave
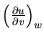 , not
, not
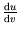 , because the first line was only true for constant
, because the first line was only true for constant 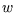 .
.
 Rearranging (2.4) also gives
Rearranging (2.4) also gives
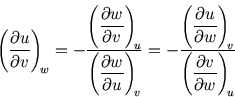 |
(2.5) |
The minus sign in these is counter-intuitive.
Equations (2.3), (2.4) and (2.5) are our main results, and may be new to you.
References





Previous: 2.12 Maxwell's Relations
Judith McGovern
2004-03-17
![]() Identify the independent variables, eg
Identify the independent variables, eg ![]() and
and ![]() .
.
![]() If
If ![]() , the partial derivative of
, the partial derivative of ![]() with respect to
with respect to ![]() is obtained by holding
is obtained by holding ![]() constant;
it is written
constant;
it is written
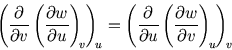
![]() by
by ![]() '' gave
'' gave
![]() , not
, not
![]() , because the first line was only true for constant
, because the first line was only true for constant ![]() .
.
![]() Rearranging (2.4) also gives
Rearranging (2.4) also gives