Efficiency of ideal gas Carnot cycle

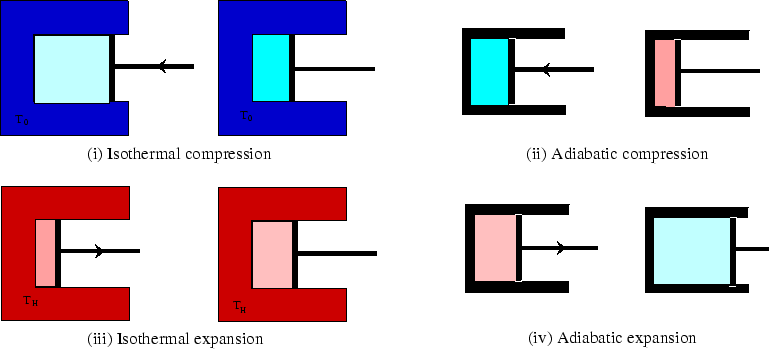
Above we see the four steps which make up an ideal gas Carnot cycle, two isothermal, (i) and (iii), and two adiabatic, (ii) and (iv). Below the cycle is sketched on a $P-V$ plot.

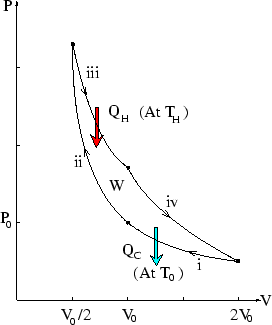
We have already analyzed this particular cycle (see here.) We worked out the work for the four steps. We note further that the heat exchanged during the isothermal steps is just minus the work done, since the internal energy is unchanged.

Thus we have $W=nR\ln 2(T_H-T_0)$ and (from stage iii) $Q_H=nRT_H\ln 2$, so

$$\eta={W\over Q_H}=1-{T_0\over T_H}.$$

Note this cycle wasn't general, because we chose to make both the isothermal and adiabatic stages volume-halving. But form of the answer is general.