Carnot wins

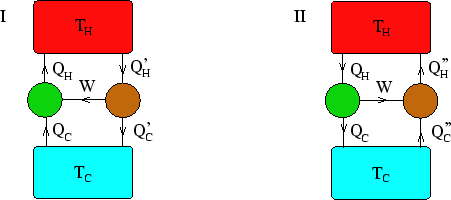
In the above the green engines/pumps are Carnot, and the brown ones are irreversible. Because the Carnot engine is reversible, if the engine efficiency is $\eta_C$, the pump efficiency is $1/\eta_C$. (See here for details.)

I) In the first case, a Carnot pump is driven by an engine. Overall, to avoid violating Clausius's statement of the second law, there must be no net heat transfer to the hot reservoir, so $Q_H'\ge Q_H$. Also, by conservation of energy, $Q_H-Q_C=Q'_H-Q'_C=W$. Thus

$$\begin{eqnarray*} {W\over Q'_H}\!\!\!&=&\!\!\!{Q_H \over Q'_H}{W\over Q_H} \\ \hbox{so}\qquad \eta_{\rm engine} &\le& \eta_{\rm carnot} \end{eqnarray*}$$

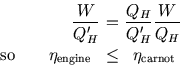
II) In the second case, a Carnot engine drives a pump. Now we need $Q_H\ge Q_H''$. Thus

$$\begin{eqnarray*} {Q''_H\over W}\!\!\!&=&\!\!\!{Q''_H \over Q_H}{Q_H\over W} \\ \hbox{so}\qquad \eta_{\rm pump} &\le& {1\over\eta_{\rm carnot}} \end{eqnarray*}$$

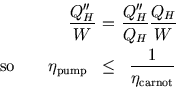
So no engine can be more efficient than a Carnot engine, and no pump can be more efficient than a Carnot pump.

If the brown pumps were in fact reversible, there could be no overall heat flow, since heat flow from a hot to a cold body is an irreversible process. In that case the inequalities would become equalities.

Thus any reversible engine working between two heat reservoirs has the same efficiency as any other.