2.1 Heat Engines and Refrigerators

Take-home message: The production of work from heat requires a temperature gradient. It is an inefficient process--most of the energy is lost as waste heat

Read an introduction to heat engines here first.

In any heat engine, heat is extracted from a hot source (eg hot combustion products in a car engine). The engine does work on its surroundings and waste heat is rejected to a cool reservoir (such as the outside air). It is an experimental fact that the waste heat cannot be eliminated, however desirable that might be. Indeed in practical engines, more of the energy extracted from the hot source is wasted than is converted into work.

The efficiency $\eta$ of a heat engine is the ratio of the work done $W$ to the heat extracted from the hot source $Q_H$:

$$\eta_{\rm engine}={W\over Q_H}$$

If $Q_C$ is the rejected heat, we have by conservation of energy

$$Q_H-Q_C=W$$

An example of an efficiency calculation for a particular cycle (the Otto cycle) can be found here.

Heat engines can also be used to pump heat from colder to hotter bodies. This always needs an input of work. Examples are fridges, air conditioners and heat pumps. These are all essentially the same, but the in the first two the purpose is to cool (or keep cool) a fridge, room or building and in the last, the purpose is to heat (or keep hot) a building. In these cases what we call the efficiency is different. In general

$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle \hbox{efficiency}={\hbox{desired output}\over \hbox{costly input}} $ }}$

In the heat engine, it is $Q_H$ that is costly (eg, petrol!) and $W$ that we want out, so as already given,

$$\eta_{\rm engine}={W\over Q_H}<1 \quad\hbox{always}$$

In the fridge or air conditioner, it is the work that is costly (electricity) and the desired result is the extraction of $Q_C$ from the room or fridge, so

$$\eta_{\rm fridge}={Q_C\over W}>1 \quad\hbox{usually}$$

In the heat pump, it is again the work that is costly (electricity) and the desired result is the addition of $Q_H$ to the building, so

$$\eta_{\rm pump}={Q_H\over W}>1 \quad\hbox{always}$$

These are sometimes called ``coefficients of thermal performance'' because students are worried by ``efficiencies'' greater than one. There would be no point in the heat pump if its efficiency, as we've defined it, were less than one--we'd just use an electric heater (efficiency exactly one) instead!

Note that real engines are optimized to perform forward or backwards, and are not reversible in the technical sense (there is friction, processes are not quasistatic). Thus relative sizes of $W$, $Q_H$ and $Q_C$ will depend on the direction. However for idealized, reversible engines only the signs will change, and we have

$\mbox{\large\colorbox{yellow}{\rule[-3mm]{0mm}{10mm} \ $\displaystyle \eta_{\rm pump}^{\rm rev}={1\over \eta_{\rm engine}^{\rm rev}} $ }}$

Often we are concerned with engines operating between only two reservoirs - one hot and one cold. In that case there is a standard way of denoting a heat engine, given below with the corresponding cycle in the $P-V$ plot. If all the arrows are reversed it represents a heat pump or fridge.

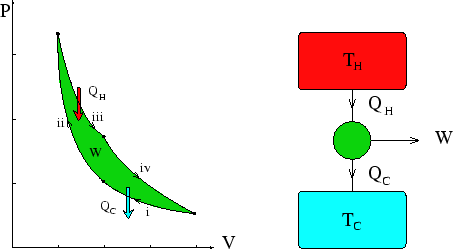
Questions about heat engines and pumps are often concerned with the most efficient possible engines, not with specific cycles. Examples of such questions can be found in the section on Carnot engines.

References

• (Mandl 5.2)
• Adkins 4.2, 4.8
• Zemansky 6.1-5